Les carrés magiques planétaires d’Agrippa revisités
- INFORMATION
- ACTUALITÉ
- ANALYSE
- EN SAVOIR PLUS
- À TÉLÉCHARGER
in De occulta philosophia (version première en 1510, 1e éd. 1531 en 2 livres, 2e éd. 1533 en 3 livres). Trad. fr. A. Levasseur 1727, revue par F. Gaboriau 1910. Trad. fr. Jean Servier : Les trois livres de la philosophie occulte ou magie, Paris, Berg International, 1981–1982,
1531
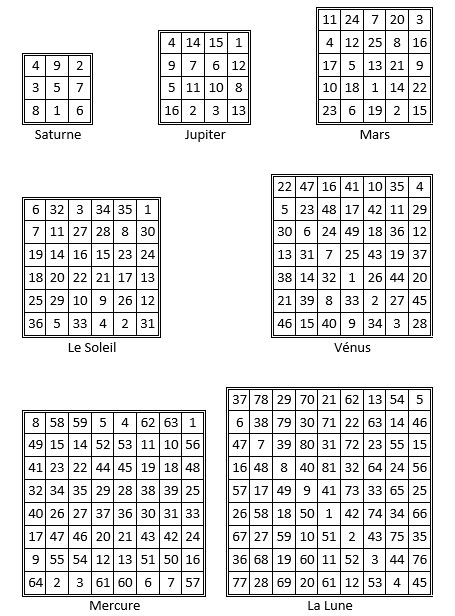
Dans le second tome, Agrippa présente entre autres sept carrés magiques normaux, d’ordre 3, 4, 5, 6, 7, 8, 9, assimilables respectivement aux planètes Saturne, Jupiter, Mars, le Soleil, Vénus, Mercure, la Lune.
Les carrés magiques planétaires d’Agrippa de Nettesheim (1486-1535).
René Descombes est Ingénieur divisionnaire honoraire des Travaux Publics de l’État – Chef d’Arrondissement honoraire du Service de la Navigation du Rhin à Strasbourg, et auteur de plusieurs ouvrages scientifiques sur les carrés magiques.

Henri Corneille Agrippa de Nettesheim (1486-1535) est originaire de Cologne, où il fit des études de lettres, droit, médecine, théologie. Il parcourt l’Europe de l’époque au service de grands personnages, tels l’empereur Maximilien, Marguerite d’Autriche, Louise de Savoie. Il est médecin à Pavie pendant un certain temps ; puis conseiller municipal et avocat à Metz, terre d’Empire, en 1518. Il exerce comme médecin à Genève, à Berne, à Fribourg. Il publie des calendriers astrologiques (1523). Il se fixe à Lyon en 1524, comme médecin ; on le retrouve cependant à Anvers en 1528. Agrippa de Nettesheim est décédé à Grenoble en 1535 ; il était âgé de 49 ans[1].

Figure 1
Son grand ouvrage, De Occulta Philosophia Libri tres, achevé dès 1510, n’est publié, en latin et en totalité, qu’en 1533, peu avant son décès. Dans le second tome, Agrippa y présente entre autres sept carrés magiques normaux, d’ordre 3, 4, 5, 6, 7, 8, 9, dont, dit-on, il ne dévoilerait pas explicitement la méthode de construction.
Agrippa parlait et écrivait huit langues : allemand, français, italien, espagnol, anglais, latin, grec et hébreu, et maîtrisait au moins autant de disciplines : astrologie, magie, lettres classiques, médecine, droit, théologie, philosophie, art de la guerre et poliorcétique, explosifs, kabbale chrétienne, exégèse, diplomatie, cryptographie, espionnage, enseignement. Ce n’était pas un scientifique, mais on peut admettre qu’il savait comment construire les carrés magiques qu’il a sélectionnés, car certaines figures de ses planches suggèrent ses méthodes de construction.
Les carrés magiques planétaires d’Agrippa
Nous nous proposons d’analyser les planches d’Agrippa, et de proposer des solutions vraisemblables pour lever le mystère apparent de la construction des carrés magiques d’Agrippa.
Les sceaux planétaires
On a associé souvent, au Moyen Age, les planètes et les métaux aux carrés magiques, en fonction de leur ordre « n », aux sceaux planétaires. Cette correspondance remonterait aux Sabéens.
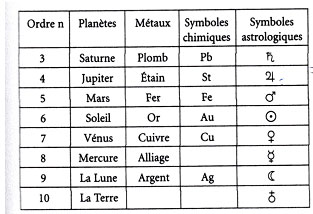
Cet ensemble de carrés magiques, de planètes et de métaux que l’on retrouve dans l’ouvrage de 1533 d’Agrippa, figure dans le livre de Lucas Pacioli (1445-1517), De Viribus Qualitatis, publié en 1490, ainsi que dans la Practica philosophia (1539) de Jérôme Cardan (1501-1576).
Or, ces anciens écrits, ces « grimoires » de magiciens, ont été rédigés bien avant l’apparition en Europe des carrés magiques comme figures mathématiques, aux xive /xve siècles. Ces « magiciens » ont fait usage de carrés magiques, liés à leurs pratiques, bien avant que les mathématiciens s’en emparent et étudient leurs propriétés arithmétiques.
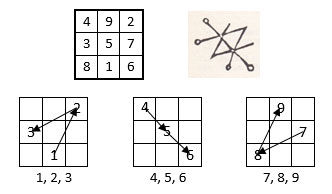
Figure 2 : L’exemple du carré magique de Saturne.
Le carré magique de Saturne (ordre 3)
La figure de la planche d’Agrippa, reproduite ci-dessus fig. 2 à côté du carré magique d’Agrippa, suggère une méthode de construction de ce carré dit de Lo Shu (il apparaît en Chine, au iie s. avant J.-C.): en décomposant ladite figure en trois phases, on inscrit ainsi les trois séries successives de 3 chiffres, 1, 2, 3 puis 4, 5, 6 puis 7, 8, 9, en suivant les tracés correspondants de chaque phase : on obtient le carré magique de Saturne.
La figure d’Agrippa pouvant être interprétée de huit façons différentes, cela conduit bien aux huit formes canoniques du Lo Shu.
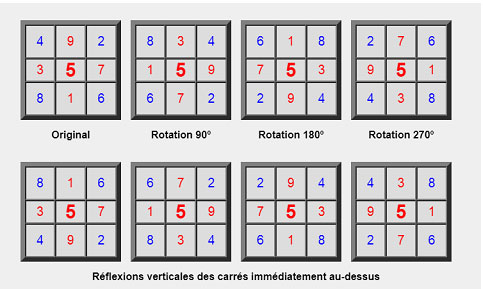
Figure3 : Pour mémoire, les formes canoniques du Lo Shu (ceci est une propriété commune à tous les carrés magiques).
Quelques propriétés spécifiques. Les chiffres des quatre alignements passant par la case centrale, sont en progression arithmétique, avec des raisons r = 1, 2, 3 et 4 ; les nombres ainsi constitués (fig. 2, diagonales et médianes : 456, 159, 258, 357) sont tous divisibles par 3 : c’est le cas de tous les nombres de trois chiffres en progression arithmétique.
La somme des carrés des chiffres des lignes extrêmes, et celles des colonnes extrêmes, sont égales entr’elles :
42 + 92 + 22 = 82 + 12 + 62 = 101
42 + 32 + 82 = 22 + 72 + 62 = 89
L’exposant « n » peut prendre les valeurs n = 1 et n = 2 dans les relations suivantes :
618n + 753n + 294n = 816n + 357n + 492n
672n + 159n + 834n = 276n + 951n + 438n
654n + 132n + 879n = 456n + 231n + 978n
852n + 174n + 639n = 258n + 471n + 938n
De plus ces relations restent vraies, lorsque l’on supprime les chiffres des centaines de tous les nombres, ou bien les chiffres des dizaines, ou bien encore les chiffres des unités. Cette propriété est vraie pour les huit formes du Lo Shu[2].
Le carré magique de Jupiter (ordre 4)
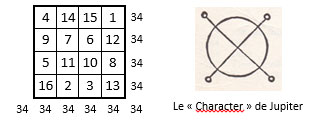
Figure 4
Une première méthode de construction : la méthode Agrippa.
- La grille-départ est le carré naturel-miroir (fig. 4, à g.)
- On considère comme invariants les nombres situés sur les deux diagonales principales.
- On échange ou permute les autres nombres symétriques par rapport au centre de la grille.
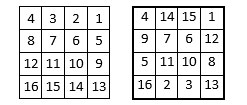
Figure 5 : Une construction du carré magique de Jupiter
Cela correspond tout-à-fait à ce que suggère la figure du « Character de Jupiter » de la planche correspondante d’Agrippa, reproduite ci-dessus (fig.4, dr.)
Donnons une autre présentation de cette méthode :
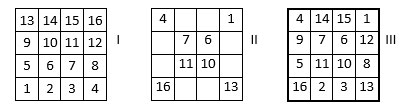
- Soit le carré naturel inversé d’ordre n = 4 (I)
- On échange ou permute les nombres situés sur les deux diagonales principales, et symétriques par rapport au centre de la grille (II)
- On complète la grille par les autres nombres qui restent à leur place (III)
@@@@@@@
La méthode de construction du père François Spinola (1562) est la suivante :
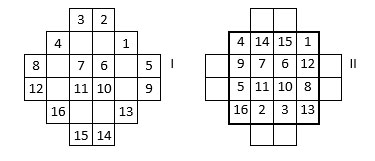
- Dans une grille crénelée d’ordre n = 4, ou place les 16 premiers entiers comme indiqué dans la figure I ci-dessus.
- On considère les nombres situés sur les diagonales principales du carré comme invariants.
- On déplace alors en croix, les couples situés aux extrémités des lignes et colonnes centrales, dans les cases libres opposées (II)
@@@@@@@
Remarquons que le carré magique de la « Melencolia » de Dürer (1514) et celui d’Agrippa (1533) sont les mêmes : il suffit de faire pivoter le carré magique d’Agrippa sur la médiane horizontale, et de permuter les deux colonnes centrales, pour obtenir le carré magique de Dürer, ou inversement.
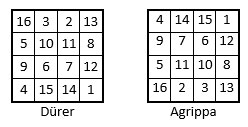
Agrippa de Nettesheim (1486-1535) et Albrecht Dürer (1471-1528) sont parfaitement contemporains. Agrippa avait rédigé sa De Occulta Philosophia dès 1510. Albrecht Dürer en avait certainement connaissance lorsqu’il a gravé la « Melencolia » en 1514. Mais on ne peut pas dire qu’Albrecht Dürer se soit inspiré d’Agrippa, comme certains le prétendent, car Dürer qui avait été initié aux carrés magiques par Lucas Pacioli di Borgo, lors de son dernier voyage en Italie, était parfaitement capable de construire lui-même le carré magique d’ordre n = 4 de la « Melencolia[3] ».
@@@@@@@
Le carré magique d’Agrippa est un carré magique de type associé[4], à constante de polarisation égale à 17. Il est à quartiers égaux, de somme M4 = 34. Le carré central de 4 cases est également de somme M4 = 34. Il y a 86 combinaisons des 16 premiers entiers pris 4 à 4 dont la somme est M4= 34. Les deux quadrilatères intérieurs ont également pour somme M4 = 34 :
9 + 15 + 8 + 2 = 5 + 14 + 12 + 3 = 34
On peut alors établir les égalités suivantes, à partir des égalités ci-dessus :
92 + 152 + 82 + 22 = 374 = 11 x 34
52 + 142 + 122 + 32 = 374 = 11 x 34
93 + 153 + 83 + 23 = 4 624 = 136 x 34
53 +143 + 123 + 33 = 4 624 = 136 x 34
Les 48 carrés magiques du Groupe I de la Classification de Frénicle, auquel appartient le carré magique d’Agrippa sous le numéro 647, possèdent naturellement les mêmes propriétés.
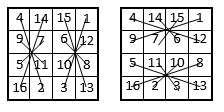
Les sommes des produits des nombres diagonaux dans les deux demi-grilles verticales sont égales, S1 = 366. Exemple (cf. ci-dessus) :
4 x 2 + 14 x 16 + 9 x 11 + 5 x 7 = 366.
Même propriété dans les deux demi-grilles horizontales, avec S2 = 246.
Le carré magique de Mars (ordre 5)
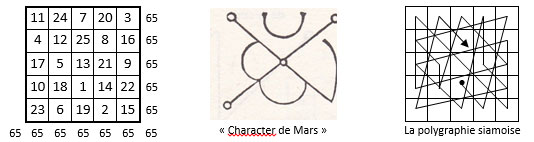
Figure 6
Les carrés magiques d’Agrippa de Mars, de Vénus et de La Lune présentent la même structure, et ont manifestement été construits par la même méthode. La méthode suggérée par Agrippa pour le carré magique de Mars apparait comme proche de la Méthode de Bachet de Méziriac, qui était connue bien avant que celui-ci l’incorpore dans son fameux ouvrage Problèmes plaisants et délectables qui se font par les nombres (Lyon, 1612).
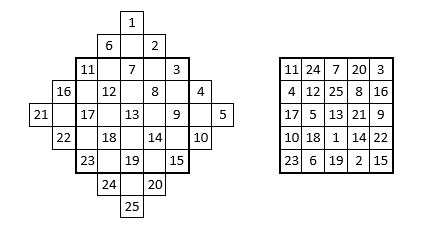
Rappelons cette méthode appliquée au Carré magique de Mars. Dans une grille crénelée d’ordre n = 5, on inscrit en oblique la série des entiers de 1 jusqu‘à n2 = 25, dans leur ordre naturel. Les nombres situés dans la grille carrée intérieure d’ordre n = 5, sont à leur place définitive, en particulier ceux situés sur les deux diagonales principales, ce que suggère bien Agrippa dans le « Character de Mars ». Dans les lignes et les colonnes, on déplace les autres nombres aux antipodes ; ces déplacements sont cependant suggérés par Agrippa de manière assez ambiguë. La somme totale des nombres de ce carré magique est ∑ = 325 = 12 + 182 = 62 + 172 = 102 + 152.
@@@@@@@
Une autre méthode. Si l’on fait abstraction des figures ou « Character » d’Agrippa, c’est la méthode bien connue sous le nom de Méthode de La Loubère, ou Méthode siamoise qui apparait clairement. Cette méthode très simple est également très ancienne.
La case-départ est située au-dessous de la case centrale de la grille d’ordre n = 5. Le cheminement régulier est normal en descendant en diagonale vers la droite (fig. 6, à dr.). L’échappement, tous les 5 sauts, se fait par 2 cases au-dessous. La polygraphie de la méthode siamoise, ci-dessus, reflète ce cheminement. Rappelons que Simon de La Loubère n’a publié son livre Du royaume de Siam qu’en 1691, dans lequel il expose cette méthode pour les carrés magiques d’ordre impair.
@@@@@@@
Encore une autre méthode. Ce carré magique normal d’ordre n = 5 peut encore être construit par la « Méthode Universelle Gilardoni » ; sans la connai alors sous ce nom, cette méthode étant peut-être connue de longue date à cette époque ?
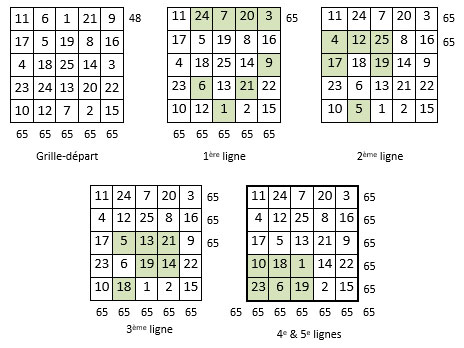
On peut très bien imaginer Agrippa recherchant, vers 1510, 5 combinaisons de 5 nombres de somme M5 = 65, dans lesquelles les 25 premiers entiers sont représentés une fois et une seule. Ce n’est pas difficile, mais nécessite un peu de patience et d’attention, en s’aidant comme « témoin » du carré naturel de même ordre ; on ne peut pas se tromper.
Voici ce qu’Agrippa aurait pu trouver, parmi les nombreuses « combinaisons magiques » des 25 premiers entiers pris 5 à 5 :

On place alors (ci-dessus) ces combinaisons dans les colonnes d’une grille d’ordre n = 5 ; on peut les placer dans un ordre quelconque : ces colonnes sont magiques par construction (puisque leurs sommes sont toutes égales). Il s’agit alors d’établir la magie des lignes, par permutation dans les colonnes, ce qui n’altère pas la magie de ces dernières. On applique alors la Méthode des colonnes initiée par Arsène Durupt.
Voici les étapes des différentes permutations dans les colonnes, ligne par ligne : les permutations dans les colonnes sont pochées en couleur. On retrouve bien le Carré magique de Mars d’Agrippa.
Quelques propriétés spécifiques du carré magique de Mars d’Agrippa. C’est un carré magique de type associé, de constante de polarisation P = 26.
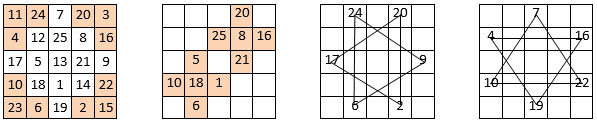
Les quatre équerres de 3 nombres (fig. ci-dessus, à g.) ont pour somme S = 39 ; on retrouve cette même somme dans les diagonales et les médianes du carré central de 9 cases. On peut insérer deux étoiles à six sommets (fig. ci-dessus, deux fig. de droite) : les nombres aux sommets des quatre triangles constituant ces étoiles, ont même somme, S = 39.
@@@@@@@
Le Problème des croix. On peut découper neuf croix de 5 cases, dont deux sont indiquées dans l’une des grilles ci-dessus (2e en partant de la g.) : dans chaque croix, la somme des 3 nombres de la branche verticale et de la somme des 3 nombres de branche horizontale sont égales ; ces sommes sont différentes dans chacune des neuf croix.
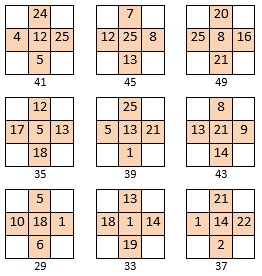
Les 9 croix définies ci-dessus, sont représentées ci-contre. Dans la grille d’ordre n = 3 de 9 cases de gauche ci-dessous, on a regroupé les différentes sommes des nombres des branches dans chacune de ces 9 croix. La Lyre correspondante[5] est représentée dans la grille suivante : on remarque que cette grille est du type associé, la constante de polarisation étant P = 78, soit le double de la case centrale. On remarque aussi que les sommes des nombres dans les médianes et les diagonales principales sont toutes égales à S = 117.
On se demande alors : cette suite de 9 nombres entiers pourrait former un carré magique ? La somme totale des 9 nombres représentant ces différentes sommes est ∑ = 351 ; la constante magique potentielle serait ainsi M3 = 351/3 = 117.
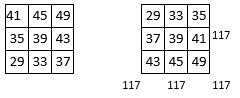 La lyre
La lyre
Notre intuition est la bonne : en effet, avec l’aide du Lo Shu comme catalyseur, on trouve 8 solutions magiques différentes, de constante magique M3 = 117 : n’est-ce pas une propriété tout-à-fait remarquable du carré magique de Mars d’Agrippa ?
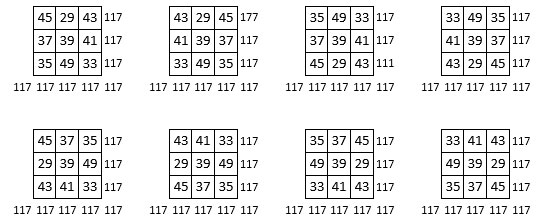
On devrait retrouver les mêmes propriétés, mutatis mutandis, dans les Carrés magiques de Vénus et de la Lune d’Agrippa.
Le carré magique du Soleil (ordre 6)
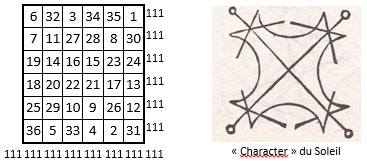
La construction du carré magique normal d’ordre n = 6 a la réputation méritée d’être difficile. Voici une interprétation du « Character du Soleil » d’Agrippa, due au général Eutrope Cazalas (1864-1943).
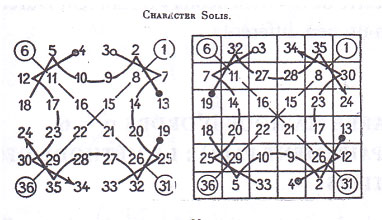
Les grilles ci-dessus permettent de suivre facilement les manipulations de cette méthode de construction, basée sur le carré naturel-miroir de même ordre, dans lequel les nombres situés sur les deux diagonales principales sont considérés comme invariants et à leur place définitive, ce que suggère bien le « Character » du Soleil. Bien sûr, on pourrait aussi construire ce carré magique d’Agrippa par la méthode Gilardoni….
@@@@@@@
Une propriété particulière. Rappelons que la somme des nombres de cette grille est ∑ = 666. Ce carré magique n’est pas de type associé, bien que de nombreux couples totalisent la même somme, S = 37 : si l’on réunit par un trait les centres des cases contenant ces couples, on obtient un tracé régulier.
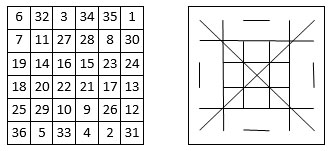
Le carré magique de Mercure (ordre 8)
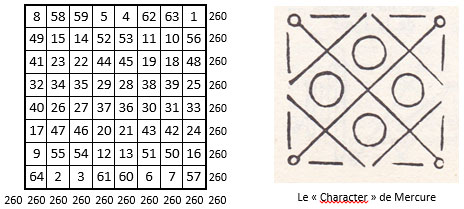
La Méthode d’Agrippa. Dans le carré naturel d’ordre n = 8, on considère les nombres situés sur les diagonales principales des quartiers comme invariants. On échange ou permute les autres nombres situés symétriquement par rapport au centre de la grille (cf. ci-dessous).
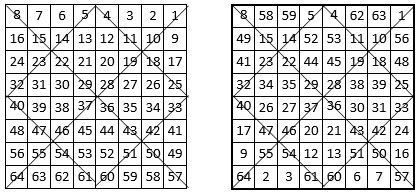
Une autre méthode (ci-dessous). Cette méthode de construction du carré magique d’Agrippa est connue sous le nom de « Méthode des pointages ».
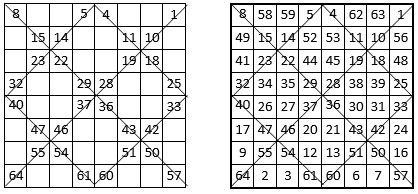
On commence à compter mentalement la série des 64 premiers entiers, depuis la dernière case de la première ligne, de droite à gauche, et on inscrit les nombres qui coïncident avec les diagonales des quartiers de 16 cases. On recommence ce comptage mental, depuis la première case de la dernière ligne, de gauche à droite, en inscrivant les nombres qui coïncident avec les cases vierges.
Le carré magique de Vénus (ordre 7)

Voici un second exemple (ci-dessous) d’application de la Méthode de Bachet de Méziriac à la construction du carré magique de Vénus, d’ordre n = 7, méthode présumée utilisée par Agrippa ! On observe en particulier que dans les alignements perpendiculaires aux premiers alignements obliques, les nombres de chaque série sont progression arithmétique de raison r = 7 = n.
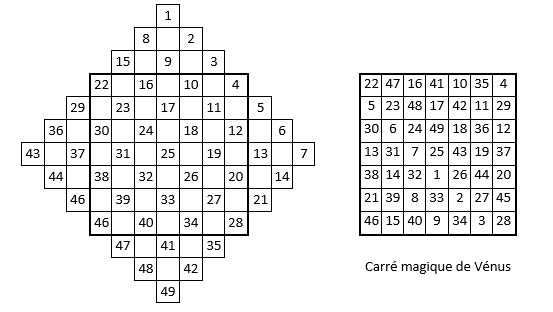
Notons une propriété particulière, déjà rencontrée dans le Carré magique de Mars. On peut former 25 croix de 5 nombres : dans chaque croix, la somme des 3 nombres situés sur la branche horizontale et la somme des 3 nombres situés sur la branche verticale, sont égales (ci-dessous). Les sommes sont différentes dans chaque croix.
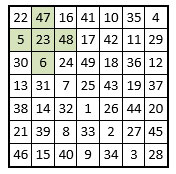
Voici, regroupées dans une grille d’ordre n = 5 de 25 cases, ces 25 sommes différentes des 25 croix découpées dans le carré magique de Vénus, avec la Lyre correspondante :
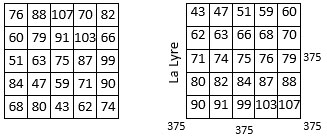
On devrait retrouver les mêmes propriétés que celles énoncées ci-dessus à propos du Carré magique de Mars, d’ordre n = 5. Ces 25 nombres devraient pouvoir être théoriquement regroupés pour former un carré magique, non normal. La somme totale de ces 25 nombres est ∑ = 1 875 ; la constante magique potentielle de ce carré magique est alors M5 = 1 875/5 = 375. Voici ci-dessous une solution sous la forme d’un carré semi-magique[6].
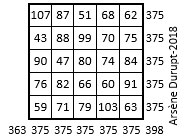
Il ne semble pas possible d’obtenir une grille magique : toutes les tentatives à ce sujet sont demeurées vaines.
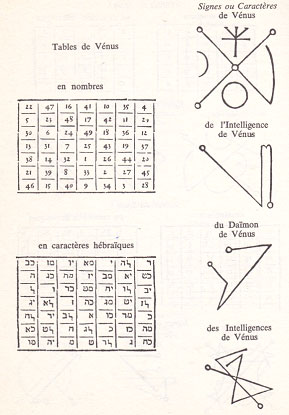
Figure 7 : Extrait de La magie céleste de C. Agrippa, traduit par Jean Servier, p. 132
Le carré magique de la Lune (ordre 9)
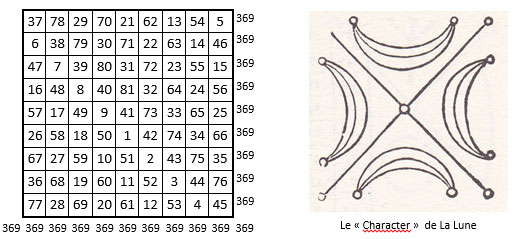
Le Carré magique de la Lune d’Agrippa, et le Carré magique que l’on trouve dans l’opuscule connu sous le nom de Enchiridion[7], rédigé vers l’an 795, par le pape Léon III, tous deux d’ordre n = 9, sont identiques.
Ces deux carrés magiques normaux de même ordre, ont-ils été construits par Agrippa en application de la Méthode Bachet de Méziriac, ou bien en application de la Méthode siamoise, qui étaient toutes deux connue de longue date ? D’aucuns prétendent qu’Agrippa aurait emprunté, vers 1510, son Carré magique de La Lune, à l’Enchiridion du pape Léon III (795) ! Sans doute Agrippa connaissait l’Enchiridion ; mais rien ne justifie cet emprunt.
@@@@@@@
Ce carré magique normal d’ordre n = 3 est de type associé, la constante de polarisation étant P = 82. Les grilles centrées d’ordre n = 3, n = 5 et n = 7 sont « magiques » sur leurs diagonales et leurs médianes.
On peut faire une autre présentation du « problèmes des croix ». On décompose ce carré magique en neuf sous-carrés de 9 cases, ce qui revient à négliger une bonne partie des 7 x 7 = 49 croix qui remplissent toute la grille :
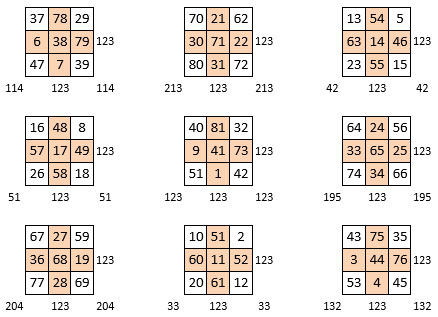
Figure 8
On observe alors les propriétés particulières suivantes :
- Les médianes ont toutes la même somme : S = 123, soit le tiers de M9 ;
- Les sommes des deux diagonales sont égales dans chaque sous-carré pris individuellement ;
- Dans le sous-carré central, les sommes des médianes et des diagonales sont égales, S = 123.

Si l’on place les sommes des diagonales des différents sous-carrés, dans une grille d’ordre n = 3 (ci-dessus à gauche), on forme directement un carré magique, non normal, de constante magique M3 = 369, et de type associé, de constante de polarisation P = 246, soit le double de la case centrale. Dans la Lyre correspondante, les nombres de chaque ligne sont en progression arithmétique de raison r = 9.

Figure 9
Les sommes totales ∑ des nombres situés dans chaque sous-carré de 9 cases (figure 6), forment à leur tour un carré magique d’ordre n = 3, de type associé, de constante magique M3 = 1 107 = 3 x 369, et de constante de polarisation P = 738 = 3 x 246. Dans la Lyre correspondante, les nombres de chaque ligne sont en progression arithmétique de raison r = 9 (figure 9).
@@@@@@@
Avec les nombres homologues[8] des 9 sous-carrés de 9 cases (cf. figure 8), on peut former neuf grilles magiques de type associé, ou semi-magiques :
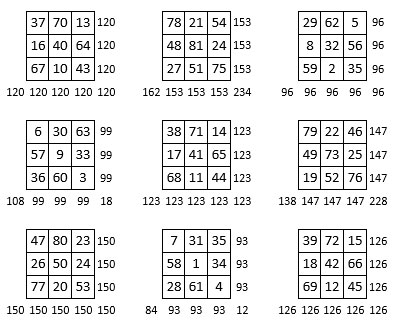
Les cinq carrés magiques de type associé se trouvent sur les diagonales de la figure ci-dessus, formée par l’ensemble des neuf sous-carrés numériques.

Les constantes magiques de ces carrés magiques ou semi-magiques, forment elles-mêmes un carré magique d’ordre n = 3, de constante magique M3 = 369 = M9, et de type associé, de constante de polarisation P = 246. Dans la Lyre correspondante, les nombres de chaque ligne sont en progression arithmétique de raison r = 3 (figure ci-dessus).
@@@@@@@
Une dernière propriété.
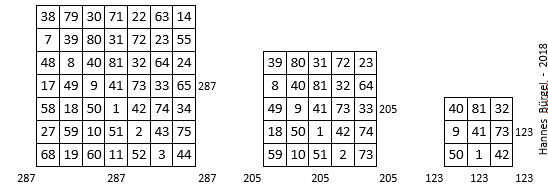
Si l’on isole les grilles carrées concentriques intérieures, d’ordre n = 7, n = 5 et n = 3, on constate que dans chaque grille, les nombres situés sur les diagonales principales et les médianes, ont une même somme.
Ainsi le Carré magique de La Lune d’Agrippa, comme le Carré magique du pape Léon III, est-il doté de propriétés remarquables.
Le carré magique de la Terre
En 1940, l’occultiste Robert Ambelain (1907-1997) compléte la série des sept carrés magiques d’Agrippa, en publiant dans sa Géomancie magique (éd. Adyard) un carré magique normal d’ordre n = 10, construit par Roger Mauduit, qui serait alors le « carré magique de la Terre ».
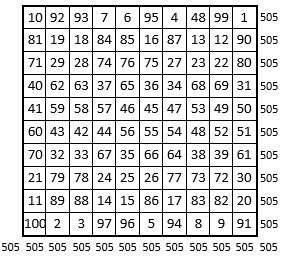
Figure 10 : le Carré magique de la Terre de Robert Ambelain, d’après Perardua 2009 (et rectifié).
Ce carré magique normal a été construit avec l’aide du carré naturel-miroir de même ordre : les nombres situés sur les diagonales principales de ce carré naturel, ceux situés sur les diagonales principales des quatre quadrants d’ordre n = 4 (16 cases), sont à leur place définitive, soit 36 nombres au total ; le placement de la plupart des autres nombres résulte de diverses permutations diamétrales ou orthogonales relativement complexes.
En conclusion, la construction des carrés magiques d’Agrippa, décryptée en partie, laisse planer encore quelques mystères. Il faut espérer que les études et recherches amorcées ici, inciteront des chercheurs à les poursuivre, pour dévoiler entièrement la pensée de Henri Corneille Agrippa de Nettesheim à ce sujet.
![]()
(janvier 2019)
[1].Cornelius Agrippa est cité à plusieurs reprises comme inspirant le jeune savant Victor Frankenstein dans le roman Frankenstein de Mary Shelley (1818).
[2]. Voir R. Holmes, Mathematical Gazette, 1970.
[4]. Un carré magique est de type associé, quand la somme des nombres symétriques par rapport au centre, pris deux à deux, est constante, alors égale à P = n² + 1 (où n est l’ordre du carré – son nombre de lignes ou colonnes). P est appelé la constante de polarisation.
[5]. On définit la lyre d’un carré magique comme le résultat du placement des termes en ordre croissant d’une ligne à l’autre, dans une grille de même ordre.
[6]. Seules les sommes des lignes et des colonnes sont égales, pas celles des deux diagonales.
[7]. Voir l’analyse BibNum par l’auteur du « Carré magique du pape Léon III » (ca 795), novembre 2014.
[8]. On appelle nombres homologues les nombres qui occupent sur une autre grille la même position qu’un nombre considéré, par exemple la position (1,1) au coin en haut à gauche, ou la position (1,2) immédiatement à droite de ce coin, et ainsi de suite.
Livres d’Agrippa
- De occulta philosophia (version première en 1510, 1e éd. 1531 en 2 livres, 2e éd. 1533 en 3 livres). Trad. fr. A. Levasseur 1727, revue par F. Gaboriau 1910. Trad. fr. Jean Servier : Les trois livres de la philosophie occulte ou magie, Paris, Berg International, 1981–1982, 3 t. : t 1 : La magie naturelle, 218 p. ; t. 2 : La magie céleste, 228 p. ; t. 3 : La magie cérémonielle, 248 p.

Sur les carrés magiques
- René Descombes, Les Carrés magiques. Histoire, théorie et technique des carrés magiques de l'Antiquité aux recherches actuelles, Vuibert, 2e éd. 2000 (494 p.)

- René Descombes, La Magie du carré. Le Carré dans tous ses éclats, Vuibert, 2004 (608 p.) [notamment la Méthode de Labosne-Méziriac, p. 409-421]

- Michel Criton & René Descombes, Nouvelles approches des carrés magiques – éditions ellipses, 2017 (402 p.) [notamment le carré magique du pape Léon III, pp. 123-131]

- Lucien Gérardin, Les carrés magiques, mystérieuses harmonies des nombres, éditions Dangles, 2e édition, 1986, 220 pp.

- Général Eutrope Cazalas, Carrés magiques au degré n, Hermann, 1934 [voir aussi article 1934 de Cazalas, « Les sceaux planétaires de C. Agrippa », Revue d’histoire des religions, JSTOR]

- René Descombes, « Une méthode universelle pour la construction des carrés magiques – La Méthode Gilardoni » (inédit).
Sur Internet
- Page Wikipédia sur les carrés magiques.

- J. Riollot, Les Carrés magiques : contribution à leur étude, Gauthier-Villars, 1907 (sur archive.org)

- René Descombes, « Le Carré magique du Pape Léon III », BibNum, septembre 2014.

- René Descombes, « À propos du carré magique d’Albrecht Dürer (1514) », BibNum, février 2016.

- René Descombes, « Le Carré magique Xi’an », BibNum, septembre 2016.

178-analyse-agrippa.pdf

texte_aggripa-178.pdf