Le Carré magique Xi’an
- INFORMATION
- ACTUALITÉ
- ANALYSE
- EN SAVOIR PLUS
- À TÉLÉCHARGER
s.o
circa XIIIe siècle
Le carré magique d’ordre 6 du palais mongol de Xi’An (Chine), aujourd’hui au musée de cette ville (il fut découvert dans les ruines du palais en 1956)
Le carré magique d’ordre 6 du palais mongol de Xi’An (Chine), aujourd’hui au musée de cette ville (il fut découvert dans les ruines du palais en 1956).

René Descombes est Ingénieur divisionnaire honoraire des Travaux Publics de l’État – Chef d’Arrondissement honoraire du Service de la Navigation du Rhin à Strasbourg, et auteur de plusieurs ouvrages scientifiques sur les carrés magiques.
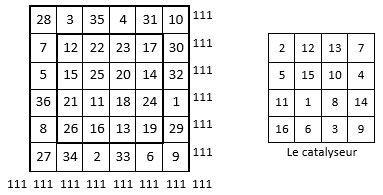
Ce carré magique, sur une plaque de fonte, a été découvert en 1956 dans les ruines d’un palais de la banlieue de Xi’an : le Palais d’Anxi, fils de l’empereur mongol Qubilai (1215-1294), lui-même un petit-fils de Gengis Khan. Cette plaque de fonte est à présent exposée au Shaanxi History Museum de Xi’an, capitale de la province du Shaanxi en Chine.
Il s’agit d’un carré magique normal, d’ordre n = 6, de constante magique M6 = 111, en caractères hindis, la numérotation écrite arabe de l’époque mongole du xiiie siècle. Ces caractères correspondent à notre système décimal, seuls les symboles des chiffres sont différents ; certains de ces symboles ressemblent cependant aux nôtres, 0, 1, 2, 3, 9.
Comment a été construit ce carré magique ?
L’auteur de ce carré magique d’ordre n = 6, un carré magique à enceinte, nous fait remarquer Arsène Durupt, est certainement parti d’un carré magique normal d’ordre n = 4, auquel il a ajouté « 10 » à chaque terme, pour former le carré numérique central dans la grille d’ordre n = 6 : ainsi ce carré magique normal d’ordre n = 4 formateur, agit-il comme un « catalyseur ».
La grille centrale obtenue est un carré magique, non normal, d’ordre n = 4 et de constante magique M4 = 74.
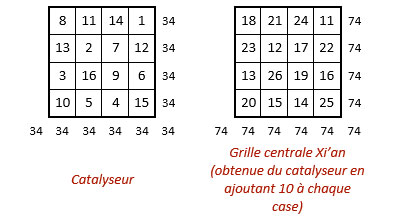
Il manque ainsi : 111 – 74 = 37 dans chaque ligne, colonne et diagonale principale pour obtenir la magie normale de la grille d’ordre n = 6 (carré Xi’an). Il reste donc à répartir dans la couronne de cette grille, les deux séries de dix nombres : 1 à 10, et 27 à 36.
On remarque que ce complément de 37 apparait comme suit dans ces deux séries, en les additionnant terme à terme :
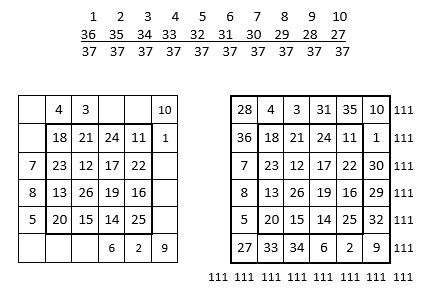
On répartit alors les nombres de la première série (1 à 10) dans la couronne, à raison de trois par côté, en prenant soin de laisser une case vide vis-à-vis de telle sorte que la somme de ces trois nombres soit la même dans les lignes 1 et 6, soit 4 + 3 + 10 = 6 + 2 + 9 = 17, et que la somme considérée soit la même dans les colonnes 1 et 6, soit 7 + 8 + 5 = 10 + 1 + 9 = 20.
Il reste alors à compléter à 37, les sommes complémentaires dans les lignes, colonnes et diagonales principales.
Le catalyseur
Le carré magique formateur ou « catalyseur », est un carré magico-magique de Fermat : c’est l’une des formes du n° 171 de la Classification de Frénicle[1] (ci-dessous). Il s’agit également du carré magique d’ordre pair dit « de Moschopoulos ».
|
1 |
12 |
6 |
15 |
|
14 |
7 |
9 |
4 |
|
11 |
2 |
16 |
5 |
|
8 |
13 |
3 |
10 |
Frénicle n° 171
Ce carré magico-magique de Fermat transmet ses propriétés spécifiques à la grille centrale Xi’an, où l’on observe en particulier (grilles ci-après) :
- Un carré magique à quartiers égaux[2] de somme S = 74 ;
- 24 formations magiques (M4 = 74) de 4 nombres, comprenant les dix alignements magiques classiques et 14 formations magiques spécifiques au carré magico-magique de Fermat, dont 4 permutations figurées, et 5 « sous-carrés francs » ;
- 32 combinaisons de 4 nombres (non magiques) dans lesquelles deux couples ont même somme dans chaque formation ;
- la somme des 8 nombres placés sur les deux diagonales principales (soit 68) est égale à la somme des 8 autres nombres de la grille ; il en est de même pour la somme des carrés et pour la somme des cubes ;
- 28 combinaisons magiques (M4 = 74) formées de deux couples de sommes égales, soit S = 37.
Ci-après, les planches numériques matérialisent dans la grille centrale magico-magique du carré magique Xian, certaines propriétés énoncées ci-dessus.

(ci-dessus) Les 24 sommes spécifiques magiques (M4 = 74) (dont les 5 sous-carrés francs) dans la grille centrale magico-magique. On remarque l’implantation géométrique spécifique des combinaisons numériques.
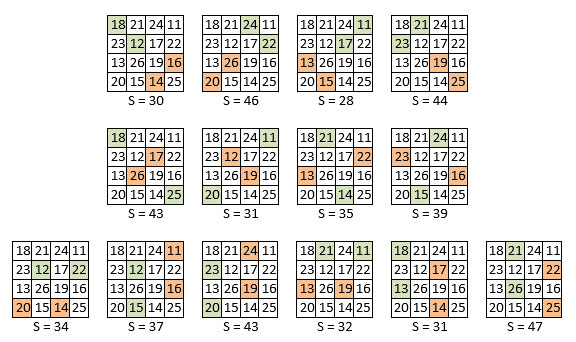
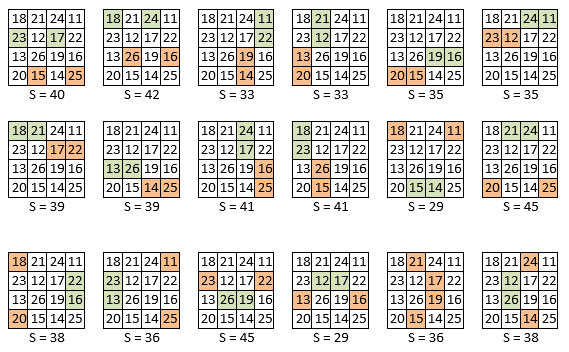
(ci-dessus) Les 32 groupes de 4 termes (non magiques) de somme S égale deux à deux.
On remarque 8 permutations figurées dans les deux premières rangées.
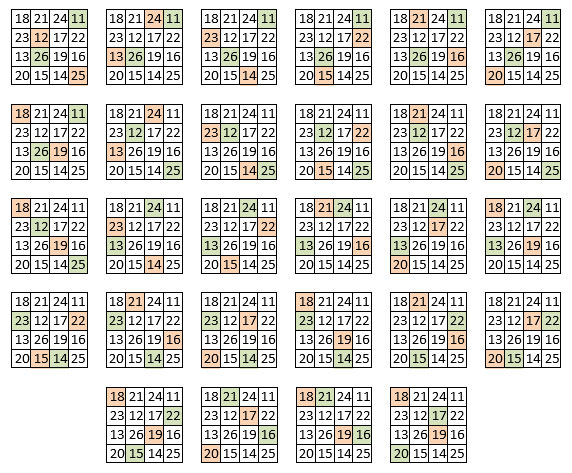
(ci-dessus) Les 28 combinaisons magiques de somme M4 = 74,
formées de deux couples de sommes égales, S = 37.
On compte huit permutations figurées.
Les propriétés spécifiques du carré magique normal d’ordre n = 6 « Xian » restent ainsi concentrées en majeure partie dans la grille centrale magico-magique d’ordre n = 4.
Un carré semi-magique de sous-carrés
Cependant, les sommes des neuf sous-carrés de 4 cases dans la grille d’ordre n = 6, forment elles-mêmes un carré semi-magique d’ordre n = 3, et de constante magique M3 = 222. La somme totale S des termes des deux diagonales principales est S = 216 + 228 = 444, soit S = 2 M3.
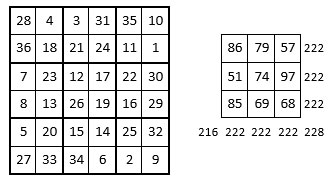
Sans oublier que les sommes des termes dans deux quartiers opposés sont égales :
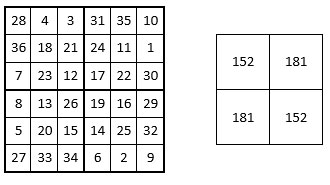
Une manip originale !
On se propose de remplir, successivement, les quadrants avec les termes homologues des 9 sous-carrés de 4 cases. Surprise : la grille obtenue, ci-dessous à droite, est un carré magique normal de mêmes caractéristiques et de mêmes propriétés que le Xi’an.
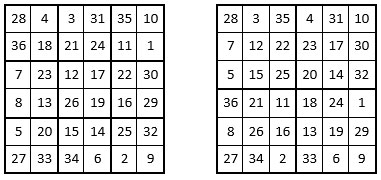
(ci-dessus) On a rempli le carré de droite avec les termes « homologues » de celui de gauche : ex. en position (H1,V2) du carré de droite, on met le nombre en position (H1,V2) du carré de gauche en tenant compte du découpage (c’est-à-dire le nombre 3).
Une généralisation
On peut implanter comme catalyseur en grille centrale, l’un quelconque des carrés magiques normaux d’ordre n = 4. Après avoir ajouté « 10 » à chaque terme, on obtient toujours un carré magique, non normal, de constante magique M4 = 74.
Il manque donc toujours 111 – 74 = 37 pour obtenir la constante magique[3] de la grille d’ordre n = 6. Il s’agit alors de remplir la couronne de cette grille, de façon indépendante de la grille centrale, avec les nombres des séries 1-10 et 27-36, en imposant la somme de 37 à deux cases vis-à-vis, tout en assurant la magie dans les lignes et les colonnes (M6 = 111). Ceci n’est pas toujours facile.
Il y a néanmoins de nombreuses solutions de remplissage de cette couronne. Voici quelques exemples différents du précédent (il en existe beaucoup d’autres). On peut ainsi considérer le carré magique Xi’an comme un cas particulier de cette méthode générale. Mais il n’est pas le seul : il y a 144 carrés magico-magiques de Fermat d’ordre n = 4, que l’on retrouve nécessairement dans la classification de Frénicle.

Un dénombrement des solutions ?
Restons tout d’abord dans le cas particulier du carré magique type « Xian ».
On peut implanter dans la grille centrale, comme catalyseur, l’un des 1 152 carrés magico-magiques de Fermat.
Lors du remplissage de la couronne, sans toucher aux nombres situés sur les diagonales, pour ne pas perturber la magie de ces diagonales dans le carré magique d’ordre n = 6, on peut permuter les 4 nombres au centre de la première ligne, et les 4 nombres au centre de la première colonne.
Cela entraine ipso facto le placement des compléments à 37 dans les cases vis-à-vis, c’est-à-dire dans la 6e ligne et la 6e colonne de la couronne. Le nombre de solutions dans la couronne est alors : 4 ! x 4 ! = 24 x 24 = 576.
Et au total le nombre N de solutions du carré magique normal d’ordre n = 6 de type « Xian » sera :
N = 1 152 x 576 = 663 552
@@@@@@@
Peut-on alors approcher, dans le cas général, un dénombrement des carrés magiques normaux d’ordre n = 6 obtenus par cette méthode ? On évalue facilement le nombre de solutions dans la grille centrale : on peut en effet choisir un catalyseur parmi les 8 formes des 880 carrés magiques normaux de base, d’ordre n = 4, de la classification de Frénicle, soit : 880 x 8 = 7 040 solutions.
Mais il est difficile d’évaluer le nombre de remplissages possibles de la couronne : c’est un très grand nombre, compte-tenu des nombreuses permutations et rotations possibles, un nombre « peut-être incalculable », pense Arsène Durupt ! Tout ce que l’on peut dire, c’est que le nombre total de solutions est un grand multiple de 7 040…
La construction du carré magico-magique normal
Il nous reste, pour être complet sur le sujet, à rappeler la construction du carré magico-magique normal d’ordre n = 4, qui est très simple.
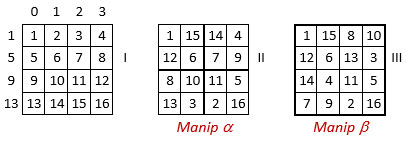
1. On part d’une table d’addition dans une grille de 16 cases, dans laquelle la somme « S » des facteurs d’addition[4] sur les deux diagonales est égale à M4 = 34, soit la constante magique du carré magique normal d’ordre n = 4. Exemple de la grille I ci-dessus (cas le plus simple du carré naturel)
2. Manipulation a : sans toucher aux nombres situés sur les deux diagonales principales de la Grille I, qui assurent la somme magique, on échange ou permute les autres nombres complémentaires ; Grille II ci-dessus.
3. Manipulation b : dans la Grille II, on permute ou échange en bloc les quartiers 2 et 3, sans toucher aux quartiers 1 et 4. La Grille III ci-dessus est un carré magico-magique[5].
Dénombrement
Si l’on permute les deux séquences de facteurs d’addition – soit, dans l’exemple ci-dessus, si l’on place la séquence horizontale ( 0 1 2 3 ) à la verticale à gauche de la grille, et la séquence verticale ( 1 5 9 13 ) au-dessus de la grille (ce qui donne la grille Ibis ci-dessous),
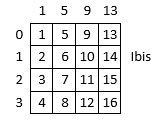
puis si l’on permute dans chaque séquence (horizontale et verticale) les quatre facteurs d’addition, on dénombre ainsi
N = 2 (4!)(4!)= 2 (4!)² = 1 152 carrés magico-magiques normaux.
@@@@@@@
Mais, en dehors de ces carrés magico-magiques normaux, il y a bien d’autres carrés dans une grille d’ordre n = 4, ayant les caractéristiques et les propriétés de ces carrés magico-magiques normaux. On peut ainsi se fixer a priori la constante magique du carré magico-magique que l’on veut construire, issu d’une table d’addition spécifique. Il y a de nombreuses solutions.
→ Application au « catalyseur » du carré magique Xi’an
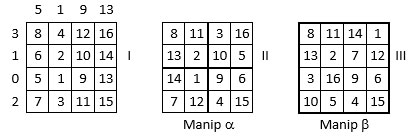
On part, par exemple, d’une table d’addition bien choisie : soit la Grille I ci-dessus, avec un carré magique d’ordre n = 4 comme catalyseur, à laquelle on fait subir la manip a ; Grille II. Sur cette Grille II, on applique la manip b : la Grille III obtenue est bien le « catalyseur » du carré magique Xi’an.
Cette construction était-elle déjà connue sous la dynastie mongole Yuan, au xiie siècle ?
(septembre 2016)
Annexe
Les 86 combinaisons des 16 premiers nombres entiers pris 4 à 4, de somme M4 = 34.
Les 28 combinaisons formées de deux couples de même somme (S = 17) sont marquées d’un astérisque [ * ]
|
1 |
1 + 2 + 15 +16* |
23 |
2 + 4 + 13 +15* |
45 |
3 + 6 + 9 + 16 |
67 |
4 + 7 + 10 +13* |
|
2 |
1 + 3 + 14 +16* |
24 |
2 + 5 + 11 + 16 |
46 |
3 + 6 + 10 + 15 |
68 |
4 + 7 + 11 + 12 |
|
3 |
1 + 4 + 13 +16* |
25 |
2 + 5 + 12 +15* |
47 |
3 + 6 + 11 +14* |
69 |
4 + 8 + 9 +13* |
|
4 |
1 + 4 + 14 + 15 |
26 |
2 + 5 + 13 + 14 |
48 |
3 + 6 + 12 + 13 |
70 |
4 + 8 + 10 + 12 |
|
5 |
1 + 5 + 12 +16* |
27 |
2 + 6 + 10 + 16 |
49 |
3 + 7 + 8 + 16 |
71 |
4 + 9 + 10 + 11 |
|
6 |
1 + 5 + 13 + 15 |
28 |
2 + 6 + 11 +15* |
50 |
3 + 7 + 9 + 15 |
72 |
5 + 6 + 7 + 16 |
|
7 |
1 + 6 + 11 +16* |
29 |
2 + 6 + 12 + 14 |
51 |
3 + 7 + 10 +14* |
73 |
5 + 6 + 8 + 15 |
|
8 |
1 + 6 + 12 + 15 |
30 |
2 + 7 + 9 + 16 |
52 |
3 + 7 + 11 + 13 |
74 |
5 + 6 + 9 + 14 |
|
9 |
1 + 6 + 13 + 14 |
31 |
2 + 7 + 10 +15* |
53 |
3 + 8 + 9 +14* |
75 |
5 + 6 + 10 + 13 |
|
10 |
1 + 7 + 10 +16* |
32 |
2 + 7 + 11 + 14 |
54 |
3 + 8 + 10 + 13 |
76 |
5 + 6 + 11 +12* |
|
11 |
1 + 7 + 11 + 15 |
33 |
2 + 7 + 12 + 13 |
55 |
3 + 8 + 11 + 12 |
77 |
5 + 7 + 8 + 14 |
|
12 |
1 + 7 + 12 + 14 |
34 |
2 + 8 + 9 +15* |
56 |
3 + 9 + 10 + 12 |
78 |
5 + 7 + 9 + 13 |
|
13 |
1 + 8 + 9 +16* |
35 |
2 + 8 + 10 + 14 |
57 |
4 + 5 + 9 + 16 |
79 |
5 + 7 + 10 +12* |
|
14 |
1 + 8 + 10 + 15 |
36 |
2 + 8 + 11 + 13 |
58 |
4 + 5 + 10 + 15 |
80 |
5 + 8 + 9 +12* |
|
15 |
1 + 8 + 11 + 14 |
37 |
2 + 9 + 10 + 13 |
59 |
4 + 5 + 11 + 14 |
81 |
5 + 8 + 10 + 11 |
|
16 |
1 + 8 + 12 + 13 |
38 |
2 + 9 + 11 + 12 |
60 |
4 + 5 + 12 +13* |
82 |
6 + 7 + 8 + 13 |
|
17 |
1 + 9 + 10 + 14 |
39 |
3 + 4 + 11 + 16 |
61 |
4 + 6 + 8 + 16 |
83 |
6 + 7 + 9 + 12 |
|
18 |
1 + 9 + 11 + 13 |
40 |
3 + 4 + 12 + 15 |
62 |
4 + 6 + 9 + 15 |
84 |
6 + 7 + 10 +11* |
|
19 |
1 + 10 +11+ 12 |
41 |
3 + 4 + 13 +14* |
63 |
4 + 6 + 10 + 14 |
85 |
6 + 8 + 9 +11* |
|
20 |
2 + 3 + 13 + 16 |
42 |
3 + 5 + 10 + 16 |
64 |
4 + 6 + 11 +13* |
86 |
7 + 8 + 9 +10* |
|
21 |
2 + 3 + 14 +15* |
43 |
3 + 5 + 11 + 15 |
65 |
4 + 7 + 8 + 15 |
|
|
|
22 |
2 + 4 + 12 + 16 |
44 |
3 + 5 + 12 +14* |
66 |
4 + 7 + 9 + 14 |
|
|
En résumé, au point de vue arithmétique, dans les 16 premiers entiers :
- On compte 86 combinaisons (magiques) de somme M4 = 34, dans les 16 premiers entiers pris 4 à 4 ;
- parmi ces 86 combinaisons, on compte 28 formations de 4 nombres de somme M4 = 34 (magiques) formées de deux couples dont les sommes sont égales à S = 17 ;
- d’autre part, et en dehors de ces 86 combinaisons, on compte 32 combinaisons de 4 nombres (non magiques ) formées de deux couples dont les sommes sont égales (et différentes de M4 = 34) dans chaque formation.
[1]. La classification de Frénicle (du mathématicien Bernard Frénicle de Bessy, 1605-1675) est une classification où sont regroupés sous le même numéro des carrés magiques similaires. Dans une classe donnée, celui qui la caractérise est le carré tel que : 1) la valeur en coin supérieur gauche est la plus petite des valeurs en coins ; 2) l'élément immédiatement à droite du coin supérieur gauche est plus petit que l'élément immédiatement sous le coin supérieur gauche.
[2]. Dans la grille centrale Xian, tous les quartiers (carrés de 4 cases dans le carré 4 × 4) ont pour somme 74.
[3]. On rappelle que la constante magique Mn d’un carré d’ordre n est Mn = n(n²+1)/2.
[4]. On appelle facteurs d’addition les ligne et rangée au-dessus et à gauche de la grille : chaque élément dans la grille correspond à l’addition des nombres émanant de cette ligne et de cette rangée.
[5]. La définition d’un carré magico-magique a été donnée plus haut (en partie ‘Le catalyseur’), avec notamment les 24 sommes magiques).
- René Descombes, Les Carrés magiques. Histoire, théorie et technique des carrés magiques de l'Antiquité aux recherches actuelles, Vuibert, 2000 (494 p.)
- René Descombes, La Magie du carré. Le Carré dans tous ses éclats, Vuibert, 2004 (608 p.)

Martin Gardner, L’univers ambidextre, les symétries de la nature, Point sciences, Seuil (1979).
- René Descombes, Le Carré naturel, problèmes et jeux, Nuvis α, 2011.
- William H. Benson & Ostwald Jacobi, New Recreations with magic squares, Dover Publications, New York, 1976.
- Bernard Gervais, Les Carrés Magiques de 5, Eyrolles, 1997
- Page Wikipédia sur les carrés magiques.
- J. Riollot, Les Carrés magiques : contribution à leur étude, Gauthier-Villars, 1907 (sur archive.org)
- René Descombes, « Le Carré magique du Pape Léon III », BibNum, septembre 2014.
- René Descombes, « À propos du carré magique d’Albrecht Dürer (1514) », BibNum, février 2016.
analyse_descombes.pdf

carre_xian.pdf





