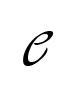analysés par les scientifiques d´aujourd´hui
Mathématiques » Théorie des nombres
Liste des textes - 6 résultats 
Les textes de Hermite (1873) rassemblés ici démontrent la transcendance de e et introduisent des méthodes nouvelles par rapport à Lambert (1761) et Liouville (1844) ; elles ouvrent la voie à la démonstration de la transcendance de Pi et de l’impossibilité de la quadrature du cercle.
Dans ce texte de trois pages, Stainville donne une démonstration du caractère irrationnel de la base des logarithmes e ; il dit tenir cette démonstration de Joseph Fourier via Poinsot.
Dans ce texte, Liouville est le premier à mettre en évidence un nombre transcendant (c’est à dire non algébrique) ; il résume cela comme « des classes très étendues de quantités dont la valeur n’est ni rationnelle ni même réductible à des irrationnelles algébriques », c’est à dire « une grande quantité de nombres qui ne sont pas algébriques ».
L’article démontre la dénombrabilité des nombres algébriques et la non-dénombrabilité des nombres réels. Il ouvre l’étude de l’infini du point de vue mathématique, marque la naissance de la théorie des ensembles – en fait une théorie de l’infini –, et porte en germe l’hypothèse du continu, premier problème de Hilbert (1900) toujours objet de recherche.
Ce texte d’une grande diversité est la preuve de l’irrationalité de π et l’acte de naissance des fonctions hyperboliques (sinus et cosinus hyperboliques).
Cantor expose les résultats qu’il a obtenus sur les nombres transfinis, c’est-à-dire les nombres (cardinaux et ordinaux) que sa théorie permet d’attribuer aux ensembles infinis. Il établit une relation d’ordre entre les cardinaux et procède aux différentes opérations avec ces cardinaux : addition, multiplication, exponentiation.
société des amis de la bibliothèque de l'X