En 1836, Joseph Liouville, formé à l'École polytechnique, puis à celle des Ponts & chaussées, est âgé de 27 ans, et il vient de fonder le Journal de mathématiques pures & appliquées, qui prend le relais des Annales de Gergonne, disparues en 1832. Brillant animateur, disposant d'un réseau de collègues dont il sollicite les publications inédites (une cinquantaine d'auteurs différents y écrivent dès les cinq premières années), il n'hésite pas à mettre lui-même, souvent copieusement, la main à la pâte : c'est ainsi que le tout premier numéro contient son « Mémoire sur le développement des fonctions ou parties de fonctions dont les divers termes sont assujettis à satisfaire une même équation différentielle du second ordre contenant un paramètre variable », premier d'une série de trois dont les deux suivants paraîtront en 1837. Quelques pages plus loin, un mémoire de son ami Charles Sturm (1803-1855), « Sur les équations différentielles linéaires du second ordre », que celui de Liouville prolonge. Les deux articles, échos de présentations légèrement antérieures à l'Académie, jettent ainsi les bases de ce que l'on appellera désormais Théorie de Sturm-Liouville.
Le premier mémoire de Liouville qu'on se propose de présenter ici est important à trois titres :
1. Il généralise de façon spectaculaire l'analyse de Fourier qui en a inspiré la genèse ;
2. Il contribue, par des lacunes inévitables pour l'époque, à ouvrir de nouvelles orientations en mathématiques au tournant du XXe siècle, avec l'étude, par Hilbert notamment, de nouveaux modes de convergence, de nouveaux espaces de fonctions ;
3. Il donne à la physique des outils essentiels, considérés aujourd'hui comme indispensables, de l'étude des vibrations mécaniques ou électromagnétiques jusqu'à la mécanique quantique.
Dès son premier numéro, le Journal de Liouville pouvait difficilement mieux justifier les deux qualificatifs de son titre : pures & appliquées. Un seul thème, décliné en deux angles d'attaque différents, chacun propre à son auteur, allait montrer dans son développement futur l'arbitraire de ces commodités de classification (et, parfois, sources de conflits universitaires...).
Le problème de Sturm-Liouville par l'exemple
Afin de mieux suivre le texte et les notations de Liouville, commençons par étudier quelques exemples explicites. Ce faisant, nous nous mettons dans les pas de Fourier et de sa théorie de la chaleur (1807, 1811), une filiation pleinement revendiquée par Liouville dès sa première phrase :
Lorsqu'on veut déterminer les lois du mouvement de la chaleur dans une barre hétérogène (…)
![Figure 1 : à droite, Joseph Fourrier [sic], en habit d’académicien. Joseph Fourier (1768 - 1830) a été Secrétaire perpétuel de l’Académie des sciences de 1821 jusqu’à sa mort en 1830. Détail de La Fée Electricité, Raoul Dufy (Palais de Chaillot, 1937). Photographie Alain Juhel.](/files/u1/Figure-1_12.jpg)
Figure 1 :
à droite, Joseph Fourrier [sic], en habit d’académicien. Joseph Fourier (1768 - 1830) a été Secrétaire perpétuel de l’Académie des sciences de 1821 jusqu’à sa mort en 1830. Détail de La Fée Electricité, Raoul Dufy (Palais de Chaillot, 1937). Photographie
Alain Juhel.
Exemple 1 : barre homogène, même température fixe aux extrémités.
La température en un point d'abscisse x, au temps t, dans une barre homogène de longueur
l (1), est régie par les équations (1), (2) et (3) :
(1)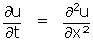
(2)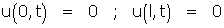
(3)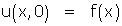
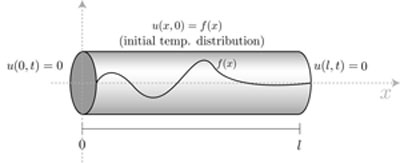
La relation (1) représente la loi d'évolution de la température dans la barre en fonction des deux variables naturelles : c'est une équation aux dérivées partielles. (2) fixe ce que l'on appelle les conditions aux limites (ici, les abscisses 0 et l). (3) fixe la donnée initiale, c'est à dire la répartition initiale des températures dans la barre : dans une de ses toutes premières expériences, Fourier l'avait uniformément chauffée (f(x) = C) avant d'installer ses extrémités dans la glace (2), et de laisser la barre se refroidir selon (1). Intuitivement, le problème semble « physiquement » bien déterminé, et l'on n'imagine guère l'expérience fournir des résultats différents si on la répète, ce que Fourier eut tout le loisir de constater. Mathématiquement, c'est dire que le problème admet une solution unique : c'est vrai, mais il n'est pas immédiat de faire la démonstration qui corrobore notre intuition physique.
Il est le plus souvent impossible, sauf dans des cas très simples, d'obtenir sous forme explicite les solutions d'équations telles que (1). Pour contourner cette difficulté, Fourier a eu, dès 1807, l'idée de séparer les variables, c'est à dire chercher des solutions de (1) sous la forme
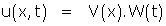
Ce faisant, il risque d’en laisser échapper beaucoup... temporairement ! Car cette forme choisie est tout ce qu'il y a de plus arbitraire. Elle n'est dictée que par la possibilité de résoudre des équations différentielles portant sur des fonctions d'une seule variable : le problème est plus simple (ou moins difficile) à traiter. Et de fait, (1) devient
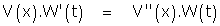
On choisit alors un
x0 et un
t0 tels que
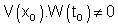
. Fixant
t =
t0, on constate que
V vérifie une équation du type
(A)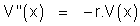
et de même, fixant x = x0 , que W vérifie une équation du type
(A')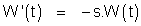
où r et s sont des réels (le signe – est une commodité). Enfin, prenant simultanément x = x0 et t = t0, on constate que r = s. On vérifie immédiatement, en retour, que ces produits fournissent des solutions de (1) ; mais on a totalement laissé de côté, pour l'instant, les conditions (2) et (3).
Pour ces solutions, vérifier (2) – pour tout t – est acquis dès que la fonction V est telle que :
(B)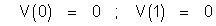
Il n'y a plus qu'à regarder si cela est possible, selon le signe de r et la forme des solutions associées :

En résumé, il n'y a de solutions non triviales que pour une famille exceptionnelle, dénombrable, de valeurs de r ; ce sont les solutions de l'équation transcendante – mais néanmoins facile ! – obtenue en x = 1
(C) 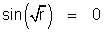
cependant que l'autre condition, en x = 0, a éliminé tout terme en cosinus.
L'équation (1) étant linéaire, toute combinaison linaire de solutions est encore solution ; cela permet d'enrichir l'ensemble des solutions de (1) et (2) en construisant des fonctions qui ne sont pas elles-mêmes des produits séparés, mais de la forme (sachant que W(t) peut être mis sous la forme e-st)
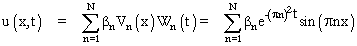
et, si l'on est un peu plus audacieux – Fourier l'était, tout en gardant un remarquable contrôle sur sa vitesse (si l'on ose dire) grâce au sens physique du problème
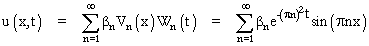
Une telle écriture en série (définie comme limite des sommes prises jusqu'à N) exige évidemment qu'on en étudie sa convergence, mais Fourier ne s'en était pas occupé, estimant que la forte décroissance des exponentielles l'assurerait quels que soient les coefficients βn.
Reste à ajuster ces coefficients, mais c'est le moment de se souvenir que la condition (3) attend toujours son entrée en scène: nous y reviendrons un peu plus loin.
@@@@@@@
Exemple 2 : une légère modification à une extrémité.
Supposons que nous considérions le même problème, modifiant seulement (2), et plus précisément la condition à la limite 1 en
(2) 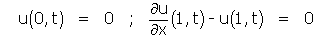
sans nous arrêter à son interprétation physique. Le traitement du problème est similaire, mais (B) est remplacée par
(B) 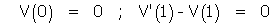
et la famille des solutions de (A) et (B) par la famille des fonctions 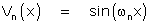 avec des donnés ωn par l'étude de l'équation
avec des donnés ωn par l'étude de l'équation
(C) 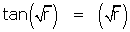
Une étude graphique convaincra, dans un premier temps, de l'existence d'une infinité dénombrable de racines ; il sera d'ailleurs facile de le démontrer par l'étude de la fonction auxiliaire tan(x) – x.
@@@@@@@
Exemple 3 : cylindre homogène, température fixée au bord.
L'équation (1) est, dans sa forme la plus générale
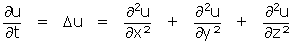
L'opérateur Δ, ou Laplacien, admet diverses expressions selon le système de coordonnées et les symétries simplificatrices du problème traité. Dans l'étude du refroidissement du cylindre homogène, seule la coordonnée radiale intervient, et l'on peut montrer que le Laplacien s'exprime par
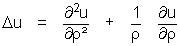
Quitte à renommer ρ en x pour mieux pouvoir comparer nos écritures dans les différents cas, la température u (x,t) est donnée par les équations (1), (2) et (3)
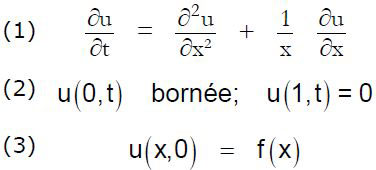
On déroule la même technique ; (1) devient
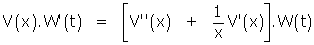
et l'on arrive – avec Fourier ! – aux équations
(A)
(A')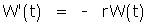
(B)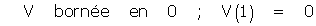
La seule différence, c'est que désormais, l'équation (A) est un peu plus difficile à résoudre. On se ramène au cas r = 1 par un changement de variable
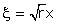
[ou
r =-1, dont on vérifie encore qu'il n'a pas de solution non triviale], et l'on reconnaît alors l'équation de Bessel, dont on sait classiquement rechercher les solutions développables en série entière, pour les lecteurs qui maîtrisent cette technique (que les autres se disent seulement que l'on obtiendra de nouvelles fonctions usuelles que l'on sait étudier et tracer, au même titre que ln ou exp). On montre que toutes les solutions bornées en 0 sont proportionnelles à celle, notée
J0 pour qui J
0(0) = 1 , à savoir
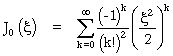
Les solutions bornées en 0 de (A) s'expriment alors par
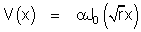
mais pour des r racines de l'équation, issue de la condition en 1, V(1) = 0
(C)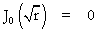
Tout ce travail a été effectué par Fourier, qui, incidemment, a donc rencontré la fonction de Bessel... dix ans avant Bessel (1817) !

Figure 2 :
Timbre allemand émis en 1984 à l’occasion du bicentenaire de la naissance de Wilhelm Bessel (1784-1846). À gauche, on reconnaît les deux premières fonctions de Bessel, JO (paire) et J1 (impaire). Image J. Miller, site
Images of Mathematicians on Postage Stamps.
Sturm et Liouville: le temps de la généralisation, la position du problème
Fourier avait ainsi constitué une collection de cas, selon la géométrie du domaine. Considérer des matériaux non homogènes rend les calculs plus volumineux, mais on obtient les mêmes groupes d'équations, ayant les mêmes significations. Liouville, qui en cela ne fait encore que suivre Sturm, est donc conduit à examiner les équations (1), (2) et (3) traduisant respectivement l'évolution, les conditions aux limites (h et H sont des constantes), et la condition initiale
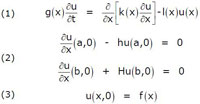
On conserve dans toute cette présentation, afin de faciliter la lecture du texte historique et la mise en correspondance des exemples précédents, les notations et la numérotation adoptées par Liouville. Nous ne ferons qu'une entorse à cette règle, en nommant a, au lieu de x (droit) et b, au lieu de X (droit, majuscule) les bornes de l'intervalle décrit par la variable ...x (italique) dans l'article de Liouville. L'exemple 1 offre un cas de l'extension mentionnée aux valeurs infinies pour h et H : diviser par h ou H efface le premier terme, puisque tout se passe comme si son coefficient était nul. La séparation des variables conduit facilement, de manière similaire, à
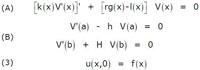
et Liouville ajoute que la réalisation de (B) impose, pour obtenir des solutions non identiquement nulles, de prendre r parmi les racines d'une équation qu'il note (p.256) :
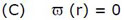
et qu'il qualifie de transcendante, car elle a, dans tous les exemples rencontrés, une infinité dénombrable de racines rn : il ne peut donc s'agir d'une équation polynomiale.
Un lecteur perspicace ne manquera pas de constater que nous ne nous sommes jamais occupés, jusqu'ici, de la condition (3) ; c'est d'elle que provient la question qui fonde l'article de Liouville. Mais d'abord, voyons ce qu'il en était dans le cas le plus simple, celui de Fourier, dans l'exemple 1. La série se traduit par
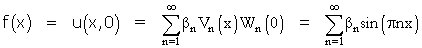
C'est sous cette forme que Fourier avait rencontré la question du développement qui porte son nom ! En d'autres termes : f étant donnée, trouver les coefficients βn convenables, et obtenir ainsi une série solution des conditions (1), (2) et (3). Le but que s'assigne Liouville, à la fin du §I de son texte, en est l'exacte généralisation :
On peut voir, dans l'ouvrage de M. Poisson sur la chaleur, comment on est porté, par la marche même du calcul, à admettre la possibilité de ce développement pour une fonction quelconque f(x) ; mais jusqu'à ce jour il a paru difficile d'établir cette possibilité directement et d'une manière rigoureuse. Je me propose de donner ici une méthode très simple pour y parvenir.
Dans l'exemple 2, il s'agit de tenter un développement, toujours en série de sinus, mais de pulsations plus irrégulières ; et dans l'exemple 3, de rechercher un développement en série de Bessel
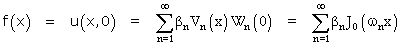
On mesure ainsi tout à la fois l'ambition du programme et la fécondité de l'approche par généralisation, qui est une première dans ce domaine.
Les prédécesseurs : Fourier, Poisson, Sturm et les autres...
De Fourier, les exemples introductifs nous ont amené à parler abondamment. La convergence de la série développant f, point mathématiquement si sensible, ne l'intéressait guère puisqu'elle n'était qu'un auxiliaire de calcul des coefficients βn qui, pour t > 0, pondéraient des exponentielles dont la forte décroissance garantissait « moralement » la convergence dans tous les cas issus de la physique : aurait-on obtenu pour tout n : βn = 1, l'écriture de f en série n'aurait eu aucun sens, mais cela n'aurait pas empêché la série de u de converger et de vérifier (1). En étudiant le problème pour lui-même, dégagé et de la source physique (la chaleur) et de la source mathématique (l'équation aux dérivées partielles), Liouville s'engage sur un terrain où l'intérêt le dispute au risque :
Cette fonction V, comme on vient de le voir, se présente utilement dans la théorie de la chaleur; mais nous la considérons ici en elle-même, abstraction faite de son usage en physique mathématique.
La première étude sérieuse de convergence est toute fraîche (Dirichlet 1829) lorsque Liouville aborde ces questions (dès 1830), et elle est d'une rigueur parfaite... mais elle requiert des hypothèses un peu trop contraignantes au goût même de son auteur.
À Poisson, Liouville doit la question du développement – et l'insuffisance de sa justification. Liouville va également exploiter, dans son calcul, des relations d'orthogonalité que Poisson est le premier à faire apparaître
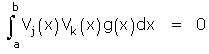
et même à étendre audacieusement à des fonctions à valeurs complexes, afin de prouver la réalité de tous les rn rencontrés.
Séparer les contributions de Sturm et Liouville semble a priori plus délicat, tant l'étude est désormais connue sous l'appellation Problème de Sturm-Liouville. Si Sturm a précédé Liouville - les dates de leurs communications respectives à l'Académie en font foi – un article à quatre mains est écrit pour le deuxième numéro du Journal de Liouville, en 1837, et la parution des articles de Sturm doit beaucoup à l'insistance de Liouville ; ce dernier le rappelait sur la tombe de son ami, lors de ses funérailles, en 1855 :
Deux beaux Mémoires sur la discussion des équations différentielles et à différences partielles, propres aux grands problèmes de la physique mathématique, ont été du moins publiés en entier, grâce à mon insistance. La postérité impartiale les placera à côté des plus beaux Mémoires de Lagrange.
Toutefois, si l'on classe les divers aspects des problèmes aux limites en trois rubriques principales:
1. Étude de la famille des valeurs rn de r donnant des solutions non triviales ;
2. étude qualitative des solutions vn associées ;
3. développement d'une fonction f donnée en série des vn ,
on peut dire que les travaux de Sturm concernent les deux premiers aspects, ceux de Liouville le troisième, comme il l'a annoncé lui-même au début de son texte.
Premier exemple de l'étude qualitative approfondie des solutions d'une équation différentielle du second ordre, les mémoires de Sturm contiennent notamment les célèbres théorèmes d'oscillation et de comparaison, grâce auxquels les points où une solution s'annule peuvent être organisés en une suite croissante : Sturm établit leur entrelacement avec les zéros d'une solution d'une équation à coefficients constants, donc aisément résoluble. Ce qui est essentiel dans un cas comme notre exemple 3, où ces zéros participent directement à la définition des rn. Dans ce cas, la théorie de Sturm montre l'oscillation de la fonction, son amortissement, et elle prouve l'existence d'une infinité de racines pour l'équation (C) .
Liouville et le développement en série de fonctions orthogonales
Un calcul purement formel – c'est à dire, fait de manipulations algébriques sans justification de convergence ni d'échange d'intégrale et de sommation, « à la Euler », pourrait-on dire – d'ailleurs, celui-ci l'avait effectué sur une série de Fourier particulière – suggère l'analyse suivante :
Si 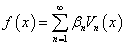 , multipliant par g(x)Vp(x) et intégrant de a à b, on aura
, multipliant par g(x)Vp(x) et intégrant de a à b, on aura
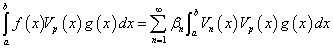
dont un seul terme subsiste grâce aux relations d'orthogonalité du type Poisson
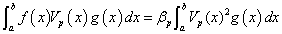
Les relations d’orthogonalité de Poisson

Figure 3 : Siméon- Denis Poisson (1781-1840)
D'où viennent de telles relations ? De deux choses :
1. de la forme très particulière, dite autoadjointe, de l'équation (A) – une équation qui n'est pas sous cette forme nécessite un petit travail de préparation pour s'y ramener;
2. des conditions aux limites (B).
En écrivant, en effet, que vn est solution de (A) pour la valeur rn sous la forme rngVn = lVn – [kV’n]’ on multiplie par Vp et on intègre de a à b
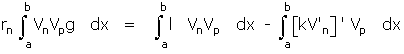
puis, par parties:
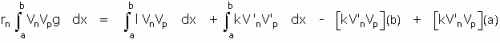
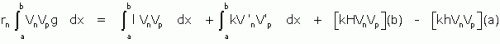
grâce aux conditions (B ); mais comme l'expression est symétrique en n et p
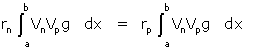
On n'intègre pas des sommes infinies comme des sommes ordinaires, quoique Cauchy, apôtre de la rigueur s'il en est, le pratique encore couramment. Les premières justifications solides viendront avec la convergence uniforme de Weierstrass (1861) : ni Fourier, ni Poisson, ni Dirichlet ne disposent d'un tel outil. Liouville n'est pas mieux loti, mais propose un autre angle d'attaque :
1. après tout, peu importe la rigueur de l'analyse, si elle nous permet de deviner la bonne formule ;
2. partons donc de la série selon la formule suggérée et appliquons toute notre rigueur à la synthèse: il suffit de sommer la série... et de trouver f.
Il insiste sur cette approche, au point de le dire deux fois, à la fin du §I d'abord, puis à celle du §II :
Sans rien supposer a priori sur l'origine de cette série ni sur sa nature, j'en cherche la valeur, et je trouve que cette valeur est f(x). Notre but, dans ce mémoire, est de trouver directement et par un procédé rigoureux la somme de la série
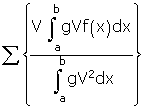
, dans laquelle le signe Σ s'étend à toutes les valeurs de r qui satisfont l'équation (C). Quelle que soit la fonction f(x), nous montrerons que la série en question a précisément pour somme f(x).
Des notations modernes : un soulagement !
Poser les notations d'un produit scalaire sur les espaces de fonctions est évidemment un anachronisme, mais quel confort le lecteur peut en retirer aujourd'hui ! Quelle satisfaction aussi de voir combien les progrès de « l'équipement technique » des mathématiques rendent accessibles et manipulables par un étudiant de premier cycle des calculs que seuls suivaient des chercheurs un siècle et demi auparavant ! Notons donc
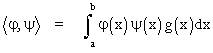
Les relations que nous avons qualifiées « d'orthogonalité » méritent cette dénomination
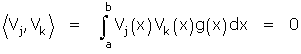
et la série dont parle Liouville s'allège en
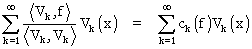
Où l'opération réussit... au prix de deux lemmes (et d'un « petit » abus) !
Pour ne pas nous égarer dans un intermède technique, sautons jusqu'au §V et regardons Liouville opérer. Avec sagesse, il donne un nom différent à la série F(x) ; il s'agit donc de montrer que F(x) = f(x).
Le calcul effectué est alors le même que celui de l'analyse, mais en remplaçant f par F, et il n'est évidemment pas mieux justifié !
Je multiplie les deux membres par
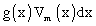
et j'intègre ensuite par rapport à x en prenant a et b pour les limites de l'intégrale.
explique-t-il. Bref, il écrit, toujours formellement, en exploitant l'orthogonalité
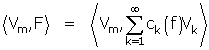
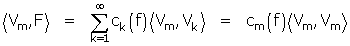
On a donc, pour tout m,
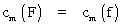
ou, en termes de produit scalaire
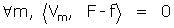
De là à conclure F = f , il n'y a qu'un pas... et c'est à ce travail que sont dévolus les lemmes.
Les lemmes ou l'espoir déraisonnable
Dans un espace géométrique de dimension 3, de base orthonormée donnée (i, j, k), un vecteur orthogonal aux trois vecteurs de la base est nul, c'est facile à prouver. Mais déjà, qu'on en oublie un, et l'on n'arrivera à rien : un vecteur orthogonal à i et j... a parfaitement le droit d'être colinéaire à k !
Il en irait de même dans tout espace de dimension finie : par exemple l'espace de fonctions combinaisons linéaires de sin x, sin 2x, ..., sin Nx, avec N fixé. Ou celui des combinaisons linéaires de V1 , V2 , ..., VN . Aussi grand soit N, pourvu qu'il soit fixé.
Mais qu'en est-il lorsqu'on s'intéresse, et c'est toujours le cas dans le problème de Sturm-Liouville, à une infinité de vecteurs orthogonaux entre eux ? En a-t-on « assez » pour conclure de même, ou ne risque-t-il pas d'en manquer, comme dans l'expérience naïve où nous n'avions pris que deux vecteurs sur trois ? - Mais hélas, de façon bien moins apparente...
Et de fait, la question ne reçoit pas toujours la même réponse. Cela a motivé la distinction des « bons » systèmes, ceux qui généralisent à la dimension infinie les « bonnes » propriétés d'une base orthonormale en dimension finie : on les appelle bases hilbertiennes, en hommage à l'étude menée par Hilbert à partir de 1904. Une des façons de les introduire est justement de les définir comme des familles totales, c'est-à-dire vérifiant l'axiome
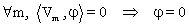
Le système des (cos n. , sin n.) de l'analyse de Fourier est un exemple de système total. Mais la preuve n'en est pas immédiate ; elle requiert des théorèmes auxiliaires importants. De façon générale, prouver la totalité d'un système n'est jamais une petite tâche anodine... c'est dire que Liouville s'attaquait – pour l'époque ! – à plus fort que lui, et que sa tentative ne pouvait qu'être vouée à l'échec. Mais, de manière bien plus positive, on doit considérer que cette lacune a beaucoup fait pour la position claire de cette question et le lancement des espaces de Hilbert.
Le lemme 2 de Liouville (§IV) affirme exactement la totalité de la famille des Vm. φ désignant toujours la fonction dont il s'agit d'établir la nullité, supposons d'abord que φ ne change de signe qu'en un nombre fini de points, a1 , a2 , ..., am-1 (Liouville n'utilise pas l'indexation, les dénommant seulement a, b, c, &c...). Il construit, grâce au lemme 1, une combinaison linéaire Ψ des possédant les mêmes zéros exactement, de même signe que φ . De la sorte,
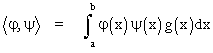
est à la fois nul et strictement positif, d'où la contradiction souhaitée.
Le lemme 1 (§IV) n'est qu'une construction progressive de Ψ à partir des Vm : annulation et changement de signe en a, b, puis en a, b, c, et ainsi de suite. C'est sans mystère.
Le « seul » problème, c'est que nous avons traité le cas d'un nombre fini de changements de signe, pas d'une infinité. Or, une fonction, même très régulière, peut posséder une infinité de zéros : l'exemple de
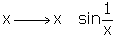
est bien connu pour être continu, et
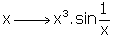
de classe C
1. Des notes ultérieures de Liouville (1840) montrent qu'il a dû concéder cette imperfection, pointée sans doute par Dirichlet.
Étape suivante : les espaces de Hilbert…
Au tournant du XXe siècle, un progrès notoire, réalisé par Hilbert (entre 1904 et 1910) et Schmidt (1907), a été d'abandonner le point de vue ponctuel pour les écritures du type
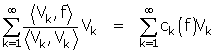
et de proposer pour de telles séries – à commencer, bien entendu, par les séries de Fourier – un sens global, l'écriture étant définie, via la norme associée au produit scalaire, par
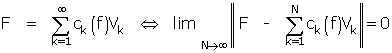
Les fonctions deviennent les vecteurs d'un
espace de Hilbert qui s'avère être le cadre naturel pour une étude à hypothèses les moins contraignantes possibles. Un théorème, dit de Hilbert-Schmidt, permet alors de récupérer, dans certains cas (dont celui du problème de Sturm-Liouville) la convergence ponctuelle, voire uniforme. L'étude spectrale, elle aussi, s'allège remarquablement : la forme autoadjointe de l'équation (A) se traduit par le caractère autoadjoint de l'opérateur D défini par
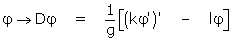
:
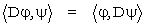
et l'orthogonalité des fonctions propres apparaît comme une conséquence générale de cette propriété.
Si cette théorie fait partie, aujourd'hui, du bagage de tout étudiant en mathématiques ou futur ingénieur, si ces espaces sont le bon cadre pour la théorie du signal, il est juste de rappeler ce que son essor doit à l'imperfection des écrits de Liouville, comme à l'urgente nécessité des applications pratiques.
Le « liouvillien » en physique quantique
Le travail d’analyse qu’a mené Liouville autour de l’équation de la chaleur de Fourier est aussi utilisé dans sa plus grande généralité en physique quantique, pour certaines résolutions de l’équation de Schrödinger. Comme le rappelle Claude Cohen-Tannoudji dans son cours au Collège de France (2), l’espace des opérateurs agissant sur l’espace ε des états d’un système quantique est appelé « espace de Liouville » et noté  . Il est défini, dans cet espace d’opérateurs, un opérateur particulier, le Liouvillien (ou « opérateur de Liouville ») : à partir de l’opérateur hamiltonien H agissant dans l’espace des états ε, on définit l’opérateur de Liouville L agissant dans l’espace
. Il est défini, dans cet espace d’opérateurs, un opérateur particulier, le Liouvillien (ou « opérateur de Liouville ») : à partir de l’opérateur hamiltonien H agissant dans l’espace des états ε, on définit l’opérateur de Liouville L agissant dans l’espace  .
.

L’opérateur de Liouville L permet d’écrire différemment certaines équations fondamentales de la physique quantique – comme celle de Schrödinger déjà citée ou celle des observables de Heisenberg – et d’aider à leur résolution :

On constate ainsi la puissance des outils créés par Liouville en analyse, utilisés en physique mathématique : les apports de Liouville à la résolution de l’équation différentielle de la chaleur sont de nos jours utilisés pour la résolution des équations de la physique quantique.
Conclusion
La portée d'un article de mathématiques ne tient pas qu'à la rigueur de ses preuves ; elle se juge aussi à la fécondité des problèmes soulevés, voire à la postérité qu'il suscite sous la forme de démonstrations complémentaires ou de nouveaux concepts. Dans la théorie des séries de Fourier, le mémoire de Fourier, malgré ou à cause de ses insuffisances, ouvre un champ de travail pour deux cents ans de mathématiques : il est du deuxième type évoqué, tandis que celui de Dirichlet marque un jalon du premier type, y compris dans l'histoire des mathématiques.
Le mémoire de Liouville, et plus généralement l'ensemble des articles que Sturm et Liouville consacrent à ce thème, procèdent des deux registres. Liouville écrit les premières pages du grand livre des développements en séries de fonctions orthogonales, dont la récente théorie des ondelettes (1980) est le dernier – et spectaculaire – avatar. Il prépare le tournant de l'analyse hilbertienne et stimule l'étude des familles orthogonales totales.
Ce même problème a inspiré à Sturm les premières études qualitatives des équations différentielles; valeurs et fonctions propres ont fait à cette occasion une entrée fracassante dans le monde des mathématiques,... et, de façon naturelle, en dimension infinie ! On s'en voudrait de l'oublier, quand tous nos enseignements (dans un louable souci de progressivité, reconnaissons-le...) abordent systématiquement ces notions dans le cadre de la dimension finie. L'histoire n'a donc pas choisi de commencer par les problèmes les plus simples...
Enfin, n'oublions pas de verser une dernière pièce, et non la moindre, à la rubrique « rigueur »: c'est dans son second mémoire que Liouville a introduit la méthode des approximations successives pour une équation différentielle du second ordre, afin de prouver l'existence et unicité d'une solution au problème avec conditions initiales, avant la généralisation qu'en donnera Émile Picard en 1890. C'est la première démarche de ce genre pour une équation du second ordre, Cauchy s'étant, quant à lui, occupé de celles du premier ordre.
Il ne sera donc pas illégitime d'appliquer à cet opus de Liouville le commentaire que Jesper Lützen fait sur l'article de Sturm: « Peu d'autres articles, en mathématiques, peuvent rivaliser avec celui-ci en termes de nouveauté du problème, des méthodes et des résultats ». Et d'ajouter, pour fêter dignement le bicentenaire de sa naissance : merci à vous, M. Liouville, d'avoir donné tant de beau travail à faire à tant de grands mathématiciens !
Juin 2010
(cet article a été publié une première fois dans le Bulletin de la SABIX, n°45, janvier 2010, consacré à Liouville ; l’encadré hors texte sur le "liouvillien", lui aussi publié dans ce Bulletin, est d’Alexandre Moatti

(1) Nous commençons, comme Fourier, par ce cas où l'équation est bien plus simple. Par ailleurs, pour des raisons de graphie comme de simplification, on prendra l = 1 par la suite.
(2) http://www.phys.ens.fr/cours/college-de-france/1975-76/1975-76.htm, Année universitaire 1975-1976, « Émission spontanée, relaxation et équation pilote », 8° leçon.
![]() )
)![]() ) Le traitement par Fourier de l’équation de la chaleur (1807,1811) allait ouvrir la voie à la « physique mathématique ». Le texte de Liouville de 1836 en est une étape importante. Il donne une méthode de résolution de cette équation, dans le cas de « variables séparables », et en élargit le champ d’application. Les méthodes de Liouville de résolution de ce type d’équations aux dérivées partielles irriguent jusqu’à nos jours des branches de recherche fécondes en mathématiques et en physique : par exemple, est utilisé en mécanique quantique (pour des résolutions de l’équation de Schrödinger) l’opérateur de Liouville, ou « liouvillien », directement issu des méthodes du présent texte.
) Le traitement par Fourier de l’équation de la chaleur (1807,1811) allait ouvrir la voie à la « physique mathématique ». Le texte de Liouville de 1836 en est une étape importante. Il donne une méthode de résolution de cette équation, dans le cas de « variables séparables », et en élargit le champ d’application. Les méthodes de Liouville de résolution de ce type d’équations aux dérivées partielles irriguent jusqu’à nos jours des branches de recherche fécondes en mathématiques et en physique : par exemple, est utilisé en mécanique quantique (pour des résolutions de l’équation de Schrödinger) l’opérateur de Liouville, ou « liouvillien », directement issu des méthodes du présent texte.
![Figure 1 : à droite, Joseph Fourrier [sic], en habit d’académicien. Joseph Fourier (1768 - 1830) a été Secrétaire perpétuel de l’Académie des sciences de 1821 jusqu’à sa mort en 1830. Détail de La Fée Electricité, Raoul Dufy (Palais de Chaillot, 1937). Photographie Alain Juhel.](/files/u1/Figure-1_12.jpg)
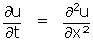
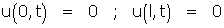
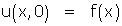

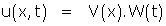
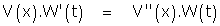
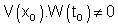 . Fixant t = t0, on constate que V vérifie une équation du type
. Fixant t = t0, on constate que V vérifie une équation du type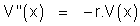
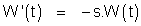
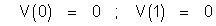

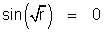
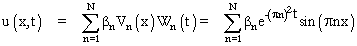
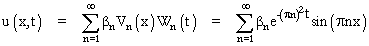
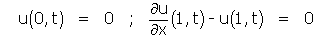
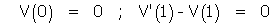
![]() avec des donnés ωn par l'étude de l'équation
avec des donnés ωn par l'étude de l'équation![]()
![]()
![]()
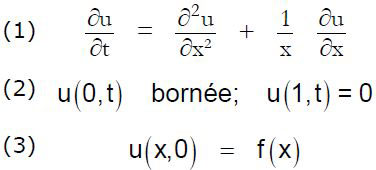
![]()
![]()
![]()
![]()
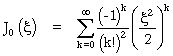
![]()
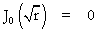

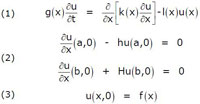
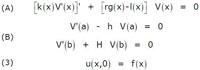
![]()
![]()
![]()
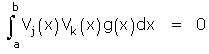
![]() , multipliant par g(x)Vp(x) et intégrant de a à b, on aura
, multipliant par g(x)Vp(x) et intégrant de a à b, on aura![]()
![]()

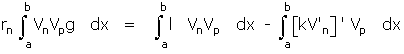
![]()
![]()
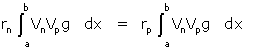
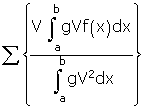 , dans laquelle le signe Σ s'étend à toutes les valeurs de r qui satisfont l'équation (C). Quelle que soit la fonction f(x), nous montrerons que la série en question a précisément pour somme f(x).
, dans laquelle le signe Σ s'étend à toutes les valeurs de r qui satisfont l'équation (C). Quelle que soit la fonction f(x), nous montrerons que la série en question a précisément pour somme f(x).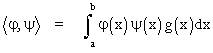
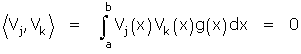
![]()
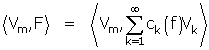
![]()
![]()
![]()
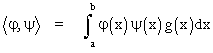
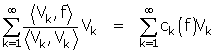
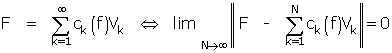
![]()
![]() . Il est défini, dans cet espace d’opérateurs, un opérateur particulier, le Liouvillien (ou « opérateur de Liouville ») : à partir de l’opérateur hamiltonien H agissant dans l’espace des états ε, on définit l’opérateur de Liouville L agissant dans l’espace
. Il est défini, dans cet espace d’opérateurs, un opérateur particulier, le Liouvillien (ou « opérateur de Liouville ») : à partir de l’opérateur hamiltonien H agissant dans l’espace des états ε, on définit l’opérateur de Liouville L agissant dans l’espace ![]() .
.


 Page consacrée à Liouville sur le site de l'auteur, avec le texte intégral des articles : http://www.mathouriste.eu/Liouville/Liouville.html
Page consacrée à Liouville sur le site de l'auteur, avec le texte intégral des articles : http://www.mathouriste.eu/Liouville/Liouville.html Initiation à l’analyse hilbertienne, sur le site de l’auteur, http://promenadesmaths.free.fr/hilbert/analyse_de_hilbert.pdf
Initiation à l’analyse hilbertienne, sur le site de l’auteur, http://promenadesmaths.free.fr/hilbert/analyse_de_hilbert.pdf










