Les conférences de Poincaré sur la T.S.F.
- INFORMATION
- ACTUALITÉ
- ANALYSE
- EN SAVOIR PLUS
- À TÉLÉCHARGER
Revue La Lumière électrique, tIV, 2e série (n°52, 26 décembre 1908), p. 387-393.
1908
Poincaré s’est intéressé aux premiers dispositifs de transmission d’ondes radio, dit « émetteurs à arc », permettant de convertir une source de courant continu en un signal électromagnétique. La première application de la T.S.F. sera la sécurité maritime (radios dans les navires).
Henri Poincaré donne des conférences à l’École supérieure des postes et télégraphes en mai-juin 1908, dans lesquelles il expose les dernières avancées de la télégraphie sans fil, domaine alors en plein essor suite à la découverte des ondes radio hertziennes en 1888. La T.S.F. aura ses premières applications dans la sécurité des bâtiments marins. Poincaré se montre intéressé, en tant qu’ingénieur de formation, aux derniers développements pratiques de cette technique (transmetteur à arc notamment), et les faisant partager à son auditoire. Il se montre aussi acteur des développements théoriques, et applique aux équations du transmetteur radio les conditions de stabilité des cycles-limites qu’il a données dans ses Méthodes Nouvelles de la Mécanique Céleste en 1892 (qu’il avait alors données pour établir la stabilité des trajectoires des planètes). C’est donc un Poincaré à la fois ingénieur et mathématicien qui apparaît à la lecture de ces conférences de 1908, récemment remises en lumière par J.M. Ginoux.
Jean-Marc Ginoux, né en 1969, est maître de conférences en mathématiques appliquées à l’IUT de Toulon. Il est docteur en mathématiques appliquées (2005) et HDR (2008), spécialiste des systèmes dynamiques non-linéaires, et auteur d’un ouvrage Differential geometry applied to dynamical systems (World Scientific, 2009). Il est aussi docteur en histoire des sciences (2011).



Les avantages de la T.S.F. par rapport à la télégraphie optique
Dans l’édition de 1907 de son ouvrage (cf. figure 1 et NbdP2), Poincaré expose p.90 de manière fort pédagogique les avantages de la télégraphie radio sans fil par rapport à la télégraphie optique (signaux lumineux) utilisée jusque là.
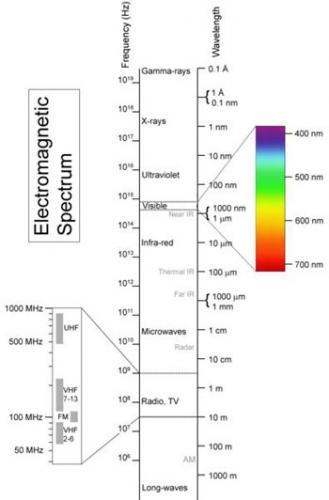
Ces avantages présentés par Poincaré sont les suivants : - longueur de parcours : « la longueur d’onde [du signal hertzien] étant plus grande [que celle du signal lumineux], la diffraction devient notable ; d’où la possibilité de contourner les obstacles. L’obstacle le plus important est celui qui est dû à la rotondité même du globe ». Ainsi, en télégraphie optique, on pouvait aller jusqu’à 50 km en choisissant des points hauts ; « avec la télégraphie sans fil, on ira à 300 km ». - le signal hertzien n’est pas arrêté par le brouillard, pour la même raison que précédemment : la lumière « est dissipée par les réflexions multiples qu’elle subit à la surface des nombreuses vésicules du brouillard (…) pour que ces réflexions se produisent, il faut que les dimensions de ces vésicules soient grandes par rapport à une longueur d’onde ». Poincaré explique : « Cette transmission facile de la lumière hertzienne à travers le brouillard est une propriété précieuse, et l’on a proposé de s’en servir pour éviter les collisions en mer ». - communication vers des postes mobiles : la communication d’un poste fixe vers un mobile est difficile avec un signal lumineux, quand on ne connaît pas la position du mobile. Pour le signal hertzien, le réglage directionnel est « long et délicat », de sorte qu’ « on ne peut guère communiquer qu’entre postes fixes (3) » ; au contraire, « des ondes hertziennes envoyées indifféremment dans toutes les directions permettront de communiquer avec un poste mobile, quand même la position n’en serait pas connue. D’où l’importance du nouveau système pour la marine ».
Poincaré souligne toutefois un inconvénient inhérent à ce dernier avantage, en temps de guerre notamment. L’ennemi peut difficilement capter un signal lumineux, directionnel et à haute altitude. « Les ondes hertziennes sont, au contraire, envoyées dans toutes les directions ; elles peuvent donc impressionner [atteindre] les cohéreurs [récepteurs] ennemis aussi bien que les cohéreurs amis et, pour le secret, on ne peut plus se fier qu’à son chiffre. De plus, l’ennemi peut troubler les communications en envoyant des signaux incohérents qui viendront se confondre avec les signaux émis par la station amie ».
Il faut ajouter que ces conférences comportent à la fois une revue des connaissances expérimentales et théoriques acquises dans ce domaine et des éléments originaux produits par Poincaré lui-même. Le meilleur exemple en est la question des ondes entretenues, sujet de la dernière conférence. L’éditorial indique :
Dans ce même éditorial sont également mentionnés la question de la symétrie de l’arc et du maintien d’une dissymétrie qui assurerait l’existence d’oscillations de toutes fréquences. Tout lecteur de la revue, ce qui inclut une grande partie des spécialistes de l’électrotechnique et de la télégraphie sans fil naissante, a donc accès à ces textes exprimés en des termes parfaitement intelligibles, clairs et synthétiques.
L’émetteur à arc
L’émetteur à arc (technologie que détaille Poincaré dans sa conférence) est un dispositif inventé en 1903 par Valdemar Poulsen (1869-1942), le même qui invente en 1900 le premier enregistreur magnétique (ancêtre du microphone). Couplé à une antenne, il permet l’émission d’un signal électromagnétique de fréquence donnée – le jaillissement d’un arc entre deux sphères était à la base des expériences de Hertz en ondes radio. L’émetteur à arc sera largement utilisé dans la radiotélégraphie naissante (notamment dans la sécurité maritime qui fut une des premières applications d’envergure), jusqu’à l’apparition des premiers tubes électroniques qui remplaceront progressivement l’émetteur à arc (celui-ci a néanmoins perduré comme émetteur de secours dans la marine jusque dans les années 1980). Il s’agit d’un des premiers convertisseurs (d’où le nom parfois donné de convertisseur à arc) de courant continu en signal radioélectrique (énergie électromagnétique rayonnée).
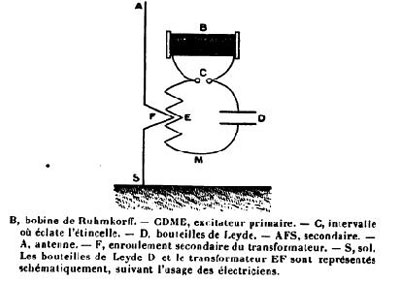
Si on place en dérivation sur un arc électrique C (jaillissant entre deux électrodes reliées à une source continue B) une capacité suivie d’une bobine d’inductance, on constate que ce circuit résonateur « LC » est le siège d’oscillations entretenues. Les oscillations entretenues sont couplées à l'antenne radioélectrique qui permet d'émettre l'onde radio à une certaine fréquence. Comme rappelle Poincaré, « il n’y pas connexion directe entre l’antenne et l’excitateur ; l’ébranlement ne se transmet à l’antenne que par induction ». Le surnom d’arc chantant a été donné par William Du Bois Duddell à ce dispositif après qu’il a pu constater que ce dernier pouvait également produire des sons (résonance à une fréquence audio donnée).
![]() (le courant x’ est la dérivée de la charge du condensateur)
(le courant x’ est la dérivée de la charge du condensateur)
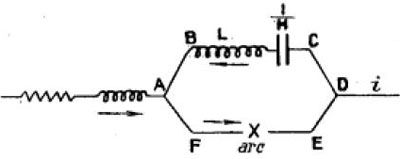
Soit ![]() l’intensité du courant dans l’arc, en appliquant la première loi de Kirchhoff (7) (1824-1887) et en tenant compte du sens du courant (voir figure 6) , il obtient :
l’intensité du courant dans l’arc, en appliquant la première loi de Kirchhoff (7) (1824-1887) et en tenant compte du sens du courant (voir figure 6) , il obtient : ![]() . Ainsi, le courant circulant dans l’arc est
. Ainsi, le courant circulant dans l’arc est ![]() . En exprimant alors, au moyen de la seconde loi de Kirchhoff (8), la tension dans la maille ABCDEF, Poincaré établit l’équation différentielle non linéaire du second ordre des oscillations entretenues par l’arc chantant
. En exprimant alors, au moyen de la seconde loi de Kirchhoff (8), la tension dans la maille ABCDEF, Poincaré établit l’équation différentielle non linéaire du second ordre des oscillations entretenues par l’arc chantant
![]() (P1)
(P1)
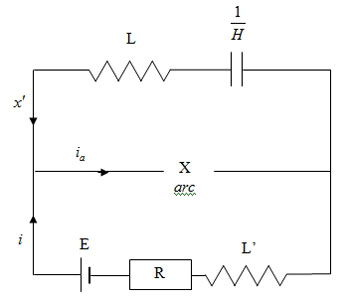
Ce dernier terme représente la force électromotrice de l’arc chantant qui est à relier à l’intensité qui le traverse par une relation déterminée empiriquement. Les controverses liées à l’existence d’une force contre-électromotrice au sein de l’arc et les difficultés inhérentes à l’expérimentation ont jeté le discrédit sur cette relation dont l’indétermination rend impossible l’intégration de l’équation (P1), comme le soulignera plus tard Paul Janet [1919]. Mais cela ne semble pas constituer un obstacle pour Henri Poincaré qui envisage le problème comme s’il était déjà résolu. Pour contourner la difficulté il exprime la tension dans la maille AFED. Une version simplifiée du circuit, présentée ci-dessous (fig. 6), permet d’appréhender l’équation qu’il obtient.
![]() (P2)
(P2)
En effet, il est facile de vérifier, à titre d’exemple, que si l’on donne à la fonction φ la forme que Poincaré lui attribue quelques pages plus loin et qui est celle de S. P. Thompson (11) : ![]() on obtient alors l’équation suivante :
on obtient alors l’équation suivante :
![]()
![]()
![]() (P3)
(P3)
![]() ;
; ![]() ;
; ![]()
L’équation (P3) devient :
![]() (P4)
(P4)
La théorie des cycles-limites de Poincaré
Un cycle limite est une orbite périodique isolée dans l’ensemble des orbites périodiques d’un système donné : Poincaré introduit cette notion dans son second mémoire de 1882 (13), à partir de ses travaux sur le problème des trois corps notamment. La représentation de l’évolution d’un système (pendule par exemple) au moyen d’une équation différentielle dans le plan de phase défini par Poincaré, c’est-à-dire, dans un espace de coordonnées tel que l’ordonnée soit la dérivée par rapport au temps de l’abscisse (par exemple (x,y) = (position, vitesse) conduit Poincaré à une classification des points fixes ou points d’équilibres du système. Il démontre alors, par analogie avec un système topographique, qu’il en existe de trois types différents (14) qu’il appelle : cols, fonds et sommets ou cols, nœud et foyer. Puis, il ajoute qu’en dehors de ces points d’équilibre il existe également des courbes qu’il nomme cycles limites et qui correspondent à des solutions périodiques pour le système considéré, dont les autres courbes définies par la même équation différentielle se rapprochent asymptotiquement sans jamais les atteindre.
![Figure 7 : Exemple de cycle limite de Poincaré [1882, p. 278]](/files/u1/Figure-7_6.jpg)
![Figure 8 : Courbe fermée, d’après Poincaré [1908, p. 390].](/files/u1/Figure-8_5.jpg)
En effet, de l’équation (P4) il est facile de tirer :
![]() (P5)
(P5)
On en déduit que, lorsque y tend vers zéro, le membre de droite de cette équation devient infini. Par conséquent, cette courbe fermée admet des tangentes verticales représentées en pointillés sur la Fig. 8. Quant au sens de parcours, le raisonnement est basé sur le fait que la dérivée d’une fonction décroissante est négative. Ainsi, lorsque x décroît, x’ devient négatif. Or en vertu de l’équation posée : x’=y. Ceci implique que y devienne également négatif. Ceci n’est possible qu’à condition de décrire la courbe dans le sens indiqué par la flèche. Il peut paraître surprenant de s’intéresser, en premier lieu, au sens de parcours de la courbe trajectoire. La raison, qui n’apparaît pas de façon évidente, est la recherche d’une condition fournie par une inégalité dont le sens va permettre de statuer sur la stabilité des oscillations entretenues. La démonstration donnée ci-dessous fait appel à la formule de Green pour l’intégration le long d’une courbe fermée ce qui nécessite de connaître le sens de parcours des courbes trajectoires pour en définir l’orientation. Poincaré présente alors une première version de la stabilité des oscillations entretenues qui est essentiellement basée sur l’existence d’une courbe fermée :
Dans la
Par comparaison avec la condition de stabilité présentée dans le texte de 1908, il apparaît clairement que « la courbe fermée » qui représente le régime stable d’ondes entretenues n’est rien d’autre qu’un cycle limite au sens où il l’a lui-même défini. On peut néanmoins s’interroger sur les raisons qui l’ont poussé à ne pas l’écrire explicitement. Cette présentation étant destinée à des ingénieurs et non à des mathématiciens, peut-être a-t-il jugé que l’introduction d’une telle terminologie n’apportait rien (16).
![]()
Or, le premier terme est sûrement positif, la fonction θ doit donc être telle que
![]() (P6)
(P6)
Cela est-il possible ? » [Poincaré 1908, p. 391]
La première équation intégrale est facile à établir. En suivant les indications de Poincaré, on multiplie l’équation (P4) par x’dt en tenant compte du fait que x’dt = dx, d’après l’équation de la page 30. On a donc :
![]()
Le premier et le dernier terme de cette équation qui correspondent à la conservation de l’énergie (½ Li² + ½ Hx²) s’annulent. La seconde inégalité intégrale se déduit du fait que le second terme quadratique est « sûrement positif » d’après Poincaré [1908, p. 391].

![]() (A1)
(A1)
Mars 2011

Remerciements L’auteur remercie Alexandre Moatti pour sa relecture et ses suggestions sur ce présent article ainsi que Christian Gérini, agrégé de Mathématiques, docteur en histoire des sciences et Bruno Rossetto, Professeur des Universités.
ANDRONOV (Aleksandr Aleksandrovich) [1929] Les cycles limites de Poincaré et la théorie des oscillations auto-entretenues, C.R.A.S., 189 (14 octobre 1929), p. 559-561.
ATTEN (Michel), DU CASTEL (François) et PIERRE (Marie) [1999] Les télécoms : histoire des écoles supérieures des télécommunications, Paris : Hachette, 1999.
BLONDEL (André) [1905a] Sur les phénomènes de l’arc chantant, C.R.A.S., 140 (13 juin 1905), p. 1680-1682. [1905b] Sur les phénomènes de l’arc chantant, Revue Générale des Sciences, 16 (1905), p. 708 ; Journal de Physique Théorique et Appliquée, (IV) 5 (1906), p. 77- 97. [1912] Henri Poincaré, La Lumière Électrique, (2e série) XIX (1912), p. 99-101. [1919] Amplitude du courant oscillant produit par les audions générateurs, C.R.A.S., 169 (17 novembre 1919), p. 943-948.
DINER (Simon) [1992] Les voies du chaos déterministe dans l’école russe, in A. Dahan. Dalmedico, J.-L. Chabert, J.-L. & K. Chemla, éd., Chaos et déterminisme, Paris : Éditions du Seuil (coll. Points Sciences), 1992, p. 331-368.
GINOUX (J.M.) & PETITGIRARD (Loïc) [2010] Poincaré’s forgotten conferences on wireless telegraphy, International Journal of Bifurcation & Chaos, vol.11 (november 2010).
JANET (Paul) [1919] Sur une analogie électrotechnique des oscillations entretenues, C.R.A.S., 168 (14 avril 1919), p. 764-766.
LEBON (Ernest) [1912] Henri Poincaré, biographie, bibliographie analytique des écrits, Paris : Gauthier-Villars (Coll. Savants du Jour), 1912.
MAISEL (von S.) [1905] Zur Theorie ungedampfter elektrischer Schwingungen, Physikalische Zeitschrift, 6 (1905), p. 38-43.
POINCARÉ (Henri) [1881] Sur les courbes définies par une équation différentielle, Journal de mathématiques pures et appliquées, (III) 7 (1881), p. 375-422, [1882] Sur les courbes définies par une équation différentielle, Journal de mathématiques pures et appliquées, (III) 8 (1882), p. 251-296, [1885] Sur les courbes définies par une équation différentielle, Journal de mathématiques pures et appliquées, (IV) 1 (1885), p. 167-244, [1886] Sur les courbes définies par une équation différentielle, Journal de mathématiques pures et appliquées, (IV) 2 (1886), p. 151-217. [1886n] Notice sur les Travaux Scientifiques de Henri Poincaré, Paris : Gauthier-Villars, 1886. [1892-93-99] Les Méthodes Nouvelles de la Mécanique Céleste, Paris : Gauthier-Villars, 1892, 1893, 1899. [1902a] Notice sur la télégraphie sans fil, Annuaire du Bureau des longitudes, p. A1- A34. [1902b] Sur la télégraphie sans fil, Revue scientifique, 17 (1902), p. 65-73. [1907] La théorie de Maxwell et les oscillations hertziennes : la télégraphie sans fil, 3e éd., Paris : Gauthier-Villars, 1907. [1908] Sur la télégraphie sans fil, La Lumière Électrique, (II) 4, p. 259-266, 291-297, 323-327, 355-359 et 387-393. [1909] Conférences sur la télégraphie sans fil, éd. La Lumière Électrique, Paris, 1909.
SIMON (Hermann Theodor) [1906] Zür Theorie des selbsttönenden Lichtbogens, Physikalische Zeitschrift, 7 (1906), p. 433-445.
VAN DER POL (Balthazar) [1926] On “relaxation-oscillations”, Philosophical Magazine, (VII) 2 (1926), p. 978-992.
ZENNECK (Jonathan) [1915] Wireless Telegraphy, New York : McGraw-Hill, 1915. [1929] The importance of Radiotelegraphy in Science, Proceedings of the Institute of Radio Engineers, 17 (1929), p. 89-114.
(1) La première édition en 1899 ne contenait pas la T.S.F. et s’intitulait simplement « La théorie de Maxwell et les oscillations hertziennes ». Il sera édité en 1904 en Anglais (« Maxwell’s theory and Wireless Telegraphy ») et réédité en 1907 (en français) (http://www.univ-nancy2.fr/poincare/bhp/pdf/hp1907tm.pdf Université de Nancy, édition de 1907)
(2) D’après Atten et al. [1999, p. 50] « Si le semestre que Henri Poincaré consacre, tous les deux ans, à des sujets particulièrement difficiles, attire nombre d'auditeurs, il n’est sans doute pas d’un intérêt immédiat pour les ingénieurs des P. et T. Mais la venue de ce physicien-mathématicien de renommée mondiale donne un éclat nouveau à l’École et c’est le but recherché par E. Estaunié : « Quand...je dus réorganiser celle-ci [l’École], il me parut qu'en recourant à Poincaré, j’avais toutes les chances de réussir mon entreprise... Il accepta de faire gratis un cours sur ... une question d’électricité à notre choix et n’ayant encore jamais été traitée... Je dois dire que la seule annonce de cette collaboration nous valut la venue de nombreux étrangers, tant étaient grands la réputation du maître et l'attrait d'un tel programme. » » Estaunié joue de ses relations pour faire inviter d’autres scientifiques de renom comme Pierre Curie (1859-1906).
(3) C’est en quelque sorte une définition des « faisceaux hertziens », largement à l’œuvre de nos jours, notamment dans les réseaux de téléphonie mobile, qui est donnée ici par Poincaré…
(4) D’après Lebon [1912, p. 67]. Les conférences de Poincaré seront ensuite publiées sous la forme d’un livre. Voir Poincaré [1909].
(5) Il s’agit du texte BibNum analysé ici, notamment ses pages 390-393.
(6) Elle avait été faite notamment par Blondel [1905]. Jonathan Zenneck [1929, p. 90], qui fut l’assistant de Karl Ferdinand Braun à Strasbourg, explique que cette équation a été initialement écrite par Kirchhoff et Lord Kelvin. De plus, on trouve dans les travaux de von S. Maisel [1904] et de Theodore Simon [1906] trace d’une équation différentielle et même de la condition de Poincaré.
(7) Loi des nœuds : le circuit à courant i se divisant en deux branches à courants respectifs i1 et i2, on a i = i1 + i2.
(8) Loi des mailles : dans une quelconque maille d'un réseau, la somme algébrique des tensions le long de la maille est constamment nulle.
(9) x’ étant une intensité, ρx’ est bien un terme de type Ri, exprimant la résistance au passage du courant.
(10) L’induction placée à côté du générateur, également appelée « self en tête » ou « self de choc», jouait un rôle analogue à celui d’une masse dans système en mouvement et avait donc pour but de produire une sorte d’inertie dans le circuit permettant ainsi d’une part de réguler la tension dans le circuit et, d’autre part de protéger le générateur. Si d’un point de vue pratique son rôle paraît indispensable sa présence dans les équations n’est pas nécessaire.
(11) Il est intéressant de remarquer que Poincaré semble être au courant des dernières hypothèses et théories concernant l’arc et notamment des travaux de Blondel [1897] puisqu’il choisit non pas la relation d’Ayrton (la plus récente) mais celle de Thompson car elle ne contient pas de force contre-électromotrice.
(12) L’équation (P3) est néanmoins incomplète à cause de l’indétermination de la fonction θ (x’).
(13) « Mémoire sur les courbes limites définies par une équation différentielle », chapitre VI (cycles limite), Journal de mathématiques, 3° série 8 (1882) p. 251-296. Voir Jean-Pierre Françoise, « La théorie des cycles limites », in L’Héritage scientifique de Poincaré (dir. E . Charpentier, E . Ghys, A. Lesne), Belin 2006.
(14) Auxquels vient s’ajouter le cas dégénéré des points de type centre.
(15) Il s’agit, à une permutation près des axes i et u, du même plan de phase que celui qu’a utilisé Blondel [1905a, p. 1681]. Ainsi, il apparaît que le cycle d’hystérésis correspond exactement à la courbe fermée de Poincaré, c’est-à-dire, à un cycle limite. (16) Le cas du centre, qui constitue également une solution sous la forme d’une courbe fermée, semble avoir été exclu par Poincaré dans la mesure où ce système est non-conservatif.
(17) Selon l’expression de Diner [1992, p. 340].
(18) La formule de Green (du nom de George Green 1793-1841) donne la relation entre une intégrale curviligne autour d'une courbe simple fermée C et l'intégrale double sur la région du plan D délimitée par C : ![]()

Poincaré, Henri, La théorie de Maxwell et les oscillations hertziennes. La Télégraphie sans fil, Scientia, 1904 (en ligne PDF Université de Nancy, édition de 1907)

Eric Charpentier, Etienne Ghys, Annick Lesne, L’Héritage scientifique de Poincaré, Belin 2006.
 Antoine Lefébure, « La T.S.F. au service de la Grande Guerre », Réseaux, Année 1986, Volume 4, Numéro 17, p. 37 – 39 (en ligne sur Persée – MESR)
Antoine Lefébure, « La T.S.F. au service de la Grande Guerre », Réseaux, Année 1986, Volume 4, Numéro 17, p. 37 – 39 (en ligne sur Persée – MESR)
Poincaré-texte.pdf

Poincare-analyse.pdf






