Le Mémoire de Fresnel sur la diffraction de la lumière

Augustin Fresnel est sans doute, avec son ami André-Marie Ampère, fondateur de l’électromagnétisme, le plus grand physicien français de la période « classique » ; celle qui précède la décennie miraculeuse 1895-1905 et le basculement vers la physique moderne. Né en 1788, dans les prémisses de la Révolution, à Chambrais, en Normandie, village qui prendra plus tard le nom du Duc de Broglie, Fresnel fait partie de ces « savants qui construisirent la République ».
C’est un personnage étonnant. Abattu par la tuberculose à l'âge de 39 ans, sa carrière était celle d'ingénieur, et son oeuvre scientifique porte sur à peine une décennie. Une vie faite de contrastes et de passion, à l'image de ces romantiques de légende emportés prématurément au début du XIXe siècle, Evariste Galois, Sadi Carnot, Frantz Schubert, Alexandre Pouchkine, Frédéric Chopin. Son oeuvre : la théorie ondulatoire de la lumière, y compris la transversalité des ondes lumineuses et la théorie de la polarisation, la théorie de la réflexion et de la réfraction, et l’optique des milieux anisotropes. Fresnel fut à la fois un expérimentateur talentueux et un théoricien profond.
Sur la nature de la lumière, seules trois adjonctions significatives interviendront après ses travaux; celle de Maxwell et la synthèse avec l’électromagnétisme en 1864 ; la théorie de la relativité d’Einstein, Lorentz et Poincaré en 1905; et la théorie quantique du rayonnement qui naît en 1900 avec Planck puis en 1905 avec le photon d’Einstein.
Un enfant attardé, brillant polytechnicien
Augustin était un enfant chétif, élevé dans un jansénisme strict par son père, Jacques Fresnel, architecte du Maréchal Duc de Broglie, qui avait épousé la fille du régisseur des domaines du duc, Augustine Mérimée. Fresnel était le cousin de Prosper Mérimée. Louis Victor de Broglie, prince, puis duc de Broglie, fondateur de la théorie ondulatoire de la matière est mort en 1987, presque deux siècles après la naissance du fondateur de la théorie ondulatoire de la lumière, né sur ses terres.
Pendant la tourmente révolutionnaire, la famille Fresnel se retire dans la maison familiale à Mathieu près de Caen. Son père Jacques (mort en 1805) s’occupait peu de ses quatre fils. L'enfant « attardé », qui ne sut lire qu’à huit ans, est pris en main par son oncle Léonor Mérimée, peintre et chimiste, futur répétiteur de dessin à l'École polytechnique, qui devient un second père pour ses neveux et découvre en Augustin des talents qu'il faut développer. Augustin fait ainsi quelques études à l'École Centrale de Caen
(1) et entre à seize ans et demi à l'Ecole polytechnique en 1804. Il y succède à son frère aîné, Louis, de la promotion 1803 (officier d'artillerie tué en 1809 au siège de Badajoz en Espagne) et y précède de trois ans son autre frère Léonor. Le dernier de la fratrie, Fulgence, sera diplomate et orientaliste.
Entré à l’X 17e, il en ressort 9e dans le prestigieux corps des Ponts et Chaussées. Il se fait remarquer par ses professeurs, Monge, Poisson, Legendre en mathématiques, Lacroix, Prony en Mécanique. Il commence sa carrière d'ingénieur des Ponts et Chaussées en 1809 à La Roche-sur-Yon. À la fin de 1812, à Nyons dans la Drôme, il participe à l'amélioration de la route impériale reliant la France à l'Italie par le Mont Genèvre.
Quelques interrogations sur la physique
Ingénieur, il aime se pencher sur des problèmes scientifiques plus fondamentaux, notamment des problèmes de physique mathématique. À partir de 1814 (à 26 ans), il se plonge dans des réflexions sur l'optique et sur la nature de la lumière: nature corpusculaire comme l'autorité de Newton l'a imposée depuis le début du XVIIIe siècle ou nature ondulatoire ? Comment en arrive-t-il là ? L’élément déclencheur vient un jour de 1814 alors qu’il lit le journal. « J'ai vu, écrit-il à son frère Léonor le 15 mai 1814, dans Le Moniteur, il y a quelques mois que Biot avait lu à l'Institut un mémoire fort intéressant sur la polarisation de la lumière. J'ai beau me casser la tête, je ne devine pas ce que c'est. »
Et sur la nature de la lumière, comme sur la polarisation, voilà Fresnel plongé dans ses pensées. Il demande des livres à son frère Léonor. Il veut se documenter, trouver des réponses à des questions que ses professeurs n'ont jamais abordées. Arago, son ami et protecteur, lui fait répondre le 12 juillet 1815 : « Je ne connais pas d’ouvrage qui renferme la totalité des expériences ... sur la lumière. M. Fresnel ne pourra se mettre au courant de cette partie de l’optique qu’en lisant l’ouvrage de Grimaldi, celui de Newton, ... et les mémoires d’Young. » Fresnel répond, le 23 septembre 1815, « Quant à l’ouvrage d’Young, ..., j’avais fort envie de le lire, mais ne sachant pas l’anglais, je ne pouvais l’entendre qu’avec le secours de mon frère [Fulgence] et, après l’avoir quitté, le livre redevenait inintelligible pour moi. »
Augustin Fresnel ne soupçonnait pas qu'au bout du compte, il serait amené à écrire lui-même le livre qu'il désirait lire.
La lumière a toujours été un phénomène physique à part, un grand mystère. Elle nous a simultanément révélé les deux grandes découvertes de la physique du XXe siècle : la relativité en 1905, et la physique quantique, avec le corps noir de Planck en 1900 et le photon d'Einstein en 1905.
La nature de la lumière a toujours été une question mystérieuse. Longtemps on a vu une parenté entre le son et la lumière, qui se répandent dans tout l’espace et sont porteurs de messages. Mais les premières véritables théories de la lumière sont venues d’un phénomène prodigieux : les rayons lumineux. Dans la nature, on ne voit ces rayons que dans des circonstances assez particulières où la lumière est partiellement occultée par des nuages ou des arbres.

Figure 1 : Rayons solaires en forêt. On peut observer le caractère rectiligne des rayons lumineux.
Le fait qu'ils soient rectilignes et qu’ils matérialisent les droites parfaites de la géométrie a toujours été considéré comme fondamental, voire sacré. Les plus anciennes religions sont de caractère astral. Le Ra de l’Egypte, l’Ahura Mazda de la Perse ancienne et Brahman, dieu suprême de l’Hindouisme, en témoignent. Dans le judaïsme et dans le christianisme, la première chose qui remplisse l’espace est la lumière. Le rayon lumineux est le chemin métaphysique vers Dieu.

Figure 2 : à gauche : Saint Sébastien, détail, par Il Sodoma (1477-1549), Galleria Pitti, Florence ; à droite : Dessin d’enfant.
C’est profondément inscrit dans l’inconscient humain. Le dessin d’enfant, figure 2, paraît banal, naturel, pas scientifique. Quantité d’enfants le dessinent ainsi. Mais quantité, c'est extraordinaire: car vous n'avez jamais vu ces rayons accrochés au soleil ! Cet enfant ne peut pas expliquer pourquoi il les a dessinés mais, pour tout le monde, leur présence est parfaitement normale !
Cela explique le développement et le succès des théories géométriques d’Euclide, Héron d’Alexandrie, Kepler, Descartes, Snell van Royen et autres. Au XVIIIe siècle, Newton décidera que la lumière est formée de corpuscules, car seuls des corpuscules peuvent se propager en ligne droite et expliquer les rayons lumineux.
Grimaldi et la diffraction
Mais depuis la fin du XVIIe siècle, on connaissait les phénomènes d’interférences et de diffraction. La diffraction fut observée par hasard par un Père jésuite, Francesco Maria Grimaldi (1618-1663). Celui-ci, observant la lumière filtrant par trou dans un volet, voit que le contour de l'image produite par un rayon de soleil, donc une « droite », n'est pas net!

Figure 3 : Diffraction par une ouverture circulaire.
Elle est au contraire agrandie et les bords en sont colorés ! La tache évoque l'aspect d'une surface liquide sur laquelle se déverserait un filet d'eau. Dans son traité, Physico-mathesis de Lumine, coloribus et iride, qui date de 1665 (deux ans après sa mort !), il conclut : « La lumière ne se propage pas seulement suivant les modes direct, réfracté et réfléchi, mais aussi suivant un quatrième : la diffraction. » Dans ce dernier mode, les rayons sont « brisés ». Grimaldi observe l’ombre d’un fil placé devant le rayon. Cette image montre, elle aussi, des ondulations parallèles au fil. Grimaldi affirme que « ... la lumière est une substance dont la propagation est susceptible de modalités ondulatoires... »
Enfin, regardant l’image formée par deux rayons adjacents proches l’un de l’autre au lieu d’un seul, Grimaldi voit que dans certaines régions où la lumière (diffractée) était visible auparavant, elle disparaît !
Lumen aliquando per sui communicationem reddit obscuriorem superficiem corporis aliunde, ac prius illustratam.
« Il arrive que de la lumière ajoutée à elle-même puisse produire des surfaces obscures sur un corps qui était éclairé auparavant. »
C’est ce que l’on nommera, un siècle et demi plus tard, des interférences. On comprend que l’
imprimatur(2) ait nécessité quelque délai !
Christian Huygens et l'autorité de Newton
Parmi les pères fondateurs de l'optique figure Christian Huygens (1629-1695). Dans son oeuvre immense, il échafauda une théorie ondulatoire de la lumière. Posant le principe que chaque point d’un front d'onde émet des ondes sphériques dont l'enveloppe donne le front d'onde à un instant ultérieur, il comprend que l’on peut expliquer les lois de Descartes pour ce qui concerne les plans d'ondes. Il comprend la périodicité en temps des vibrations, mais n'a la notion ni de longueur d'onde ni d'interférences. Sa théorie ne peut expliquer l'existence de rayons lumineux, mais il obtient d'étonnants résultats en faisant l'hypothèse de vibrations d'un "éther" élastique. Son triomphe est l'explication de la double réfraction à l'aide d'un modèle moléculaire des milieux anisotropes : il montre qu'il existe deux types de surfaces d'onde, donc deux indices de réfraction
(3) !
Mais Newton avait un caractère difficile. Secret, souvent mesquin, il écrase Huygens, jeune continental qui l’insupporte. Huygens sera aux oubliettes jusqu'à ce que Fresnel l'en fasse revenir.
Après bien des détours et ambiguïtés, Newton énonce une théorie corpusculaire, la théorie de l'émission. Comme en mécanique, la lumière est constituée de molécules de lumières, émises par les corps lumineux. Cette idée s‘impose, dit-il, car elle seule explique les rayons lumineux : les molécules de lumière se propagent en ligne droite.
Certes, il côtoie, il pratique les phénomènes d'interférences (les anneaux de Newton, les couleurs des couches minces découvertes en 1666 par son ami Hooke, rapidement excommunié) mais il nie l'explication ondulatoire. Il attribue ces effets à des « accès de facile réflexion et de facile transmission » de la lumière.
Pour Newton, la diffraction provient de l'attraction entre la lumière, qu’il estime pesante, et le bord de l'écran, cette attraction étant de courte portée et se limitant donc aux rayons lumineux proches du bord. La diversité des couleurs provient d'une différence de densité et de taille entre des particules lumineuses spécifiques.
Le XVIIIe siècle restera étonnamment fidèle à l'hypothèse newtonienne.
Le retour de la théorie ondulatoire
Le médecin anglais Thomas Young (1773-1829) fut le premier à se livrer à la critique des idées de Newton, et à prôner un retour à l'hypothèse ondulatoire, à la suite de sa célèbre expérience d'interférences en 1802. Young était un esprit universel prodigieusement doué
(4).
Mais cela, Fresnel, en 1814, ne le savait pas ! Le blocus continental freinait les échanges scientifiques.
Le retour de Napoléon de l'île d'Elbe permit, paradoxalement, à ces idées de prendre tournure. Fresnel en effet, comme beaucoup de ses camarades de l'X, se dressa publiquement contre l'Empereur, qualifiant les Cent Jours d' « attaque contre la civilisation »
(5). Révoqué du Corps des Ponts (il sera réintégré en juillet 1815) et mis sous surveillance policière, Fresnel rejoint la maison familiale de Mathieu et consacre ce loisir forcé à ses expériences et réflexions sur la diffraction de la lumière.
À Mathieu, ses premières investigations concernent l'étude expérimentale de la diffraction. Ces études sont le prélude d’une décennie de travaux qui déboucheront sur une théorie complète des propriétés de la lumière.
Le texte que nous commentons ici est son tout premier mémoire, adressé à l’Académie des sciences le 15 octobre 1815, et examiné par Arago et Poinsot. D’un enthousiasme quasi-juvénile, il contient l’essentiel de ses intuitions et de leur vérification, même s’il renferme des inexactitudes, voire des fautes qui amplifient la dimension humaine du personnage et son cheminement intellectuel. Entre ce premier travail et le grand mémoire du 29 juillet 1818 couronné par l’Académie en 1819, et qui fait encore autorité, il y a des changements notables, dont nous soulignerons l’essentiel. L’intérêt de ce premier travail est d’avoir déclenché quantité de réactions. C’est après avoir reçu les critiques et avis de ses collègues Arago, Poisson, Laplace, Ampère et d’autres et après avoir déposé un pli cacheté important à la séance du 20 avril 1818, pli ouvert quatre ans plus tard, qu’il est parvenu au texte final. De nombreux textes, dont des lettres, figurent dans le premier volume de ses Œuvres complètes auquel on peut se référer.
Ce mémoire de 1815 est d’abord une attaque en règle contre la théorie de Newton et donne l'impression d'un immense défi à 120 ans de distance (il disait avec irrespect pour le grand homme, que « Newton radote »).
Fresnel, une attaque en règle contre Newton
Le mémoire de 1815 comporte une succession de « coups de griffe » du jeune savant de 27 ans à l’égard de l’illustre Newton : §3 : « La théorie de Newton conduit à plusieurs hypothèses improbables » §6 : « La double réfraction a obligé Newton de faire encore une hypothèse, qui est bien extraordinaire » §7 : « Il me semble que la théorie des vibrations se plie mieux que celle de Newton à tous les phénomènes.» §16 : « Cette conséquence (…) est tout à fait opposée à la thèse de Newton, et confirme la théorie des vibrations.» §26 : « Et c’est ce qui a été cause sans doute de l’erreur où est tombé Newton.» §38 note : « Newton est obligé de supposer que la lumière peut être repoussée à une distance sensible des corps.» §42 : « Je tire de cette théorie une conséquence absolument opposée à celle de Newton.» La phrase conclusive en §45 : « Cette théorie des vibrations (…), qui lie déjà tant de phénomènes séparés dans celle de Newton, ne doit-elle pas conduire à la véritable explication de la polarisation.» Et enfin la lettre d’envoi du 15 octobre 1815 au Secrétaire perpétuel Delambre :« La théorie de Newton est encore adoptée généralement. Je ne connais aucun ouvrage dans lequel elle soit attaquée directement, et où l’on donne, ainsi que je l’ai fait, les formules pour calculer la largeur des franges colorées des ombres. »
C’est en évoquant Newton que Fresnel débute son mémoire (§1) :
J’exposerai sommairement les principales objections que je me suis faites sur la théorie newtonienne. Newton ayant posé en principe que les molécules de lumière qui frappent nos yeux, lorsque nous regardons le soleil, partent de cet astre pour arriver jusqu'à nous, fut obligé de supposer que leur marche n'est point dérangée par les molécules de calorique répandues dans l'espace.
Notons l’apparition du mystérieux « calorique ». Il s’agissait, à l’époque, d’une conception de la chaleur comme un fluide s'écoulant des corps chauds vers les corps froids
(6). Fresnel le concevra comme étant le milieu dans lequel se propagent les vibrations lumineuses, avant de le remplacer par l’éther, encore plus mystérieux, qui mènera toutefois à la relativité.
... Lorsqu’un corps noir est exposé à l'action de la lumière ... Il ne peut pas en absorber éternellement, et, après s’en être saturé, il devrait en rendre autant qu’il en reçoit. Que devient donc la lumière ? Il la rend à l’état de calorique. Ce n’est qu’en admettant l'identité des molécules de la lumière et du calorique qu’on peut concevoir le phénomène.
(On savait que le rayonnement lumineux pouvait être absorbé par des surfaces sombres et les chauffer. On savait aussi qu’il existait un régime et une température d’équilibre pour un corps et un rayonnement donnés.)
Une molécule lumineuse qui traverse l'atmosphère doit donc éprouver continuellement des répulsions qui contrarient son mouvement. Comment peut-il se faire que toutes ces répulsions ne contrarient pas sa vitesse, et qu'en donnant du mouvement à tant de milliards de molécules elle ne finisse pas par perdre le sien? »
La physique quantique et relativiste rend cocasse une des objections de Fresnel à propos de la biréfringence, que nous avons déjà mentionnée:
La double réfraction a obligé Newton à une hypothèse bien extraordinaire: que les molécules lumineuses aient des pôles et que le spath d'Islande tourne d'un même côté les pôles de même espèce.
En un sens, ici Newton avait raison. Mais ni lui ni Fresnel ne pouvait deviner que la polarisation de la lumière provient du fait que le
photon d’Einstein, particule de masse nulle, possède une « rotation quantique » sur lui-même, appelée
spin ou
hélicité(7).
Mais le point central est le suivant :
La plus forte objection qu'on ait faite à cette théorie est celle qui est fondée sur la comparaison de la lumière et du son. (...) Cette objection, la seule à laquelle il me paraisse difficile de répondre complètement m'a conduit à m'occuper des ombres portées ... j'ai observé que les ombres n'étaient jamais terminées nettement comme elles devraient l'être si la lumière ne se propageait que dans le sens de sa direction primitive. On voit qu'elle se répand dans l'ombre, et il est difficile d'assigner le point où elle s'arrête, les limites de l’angle d’inflexion. J’ai vu de la lumière jusque dans le milieu de l’ombre d’une règle de deux centimètres de largeur.
Dans son grenier, Fresnel se met au travail avec un appareillage fait de ses mains. Le serrurier et le forgeron du village l’aident dans son entreprise.
Il observe d'abord l'ombre portée à longue distance d'un fil de fer éclairé par une source ponctuelle. Que la source soit ponctuelle est essentiel car cela protège des effets de pénombre des sources étendues. Il intercepte un rayon de soleil filtrant par ses volets avec une lentille de forte courbure placée derrière un petit trou, ce qui diminue la gêne causée par le mouvement du soleil.
Je me suis d’abord servi, pour obtenir un point lumineux, d’un très petit trou fait dans une feuille d’étain... N’ayant pas de plus forte lentille pour obtenir un point lumineux plus fin, je me suis servi d’un globule de miel déposé sur un petit trou fait à une feuille de cuivre.
Le « fil de fer » est une fine lame biseautée sur chacun de ses côtés, ce qui permet de s’assurer que sa largeur est constante. On mesure les ombres à des distances extrêmement variables du fil (entre 1,033 et 5, 267 m), le fil étant lui-même à des distances variables de la source de lumière (entre 1,7 cm et 8,46 m).
Fresnel observe la structure de l’ombre et des franges qu’elle comporte sur un écran : carton, verre dépoli. Pour mesurer la position des franges avec la plus grande précision, il fabrique un micromètre (§20, pages 19 et 20).
J’ai construit un micromètre avec lequel je puis mesurer les largeurs des ombres à moins d’un quarantième de millimètre près. Il est formé de deux fils de soie partant d’un même point et aboutissant à deux points éloignés l’un de l’autre de cinq millimètres.... Un petit carton mobile me sert à marquer l’endroit où la distance des fils est égale à la largeur de l’ombre. Le cadre qui porte ces fils ... a 218 millimètres de longueur, je puis donc évaluer la distance entre les fils à moins d’un quarantième de millimètre.
Fresnel se préoccupe de façon méticuleuse de la précision de ses mesures. Les estimations d’erreurs qu’il donne dans cet article ont permis à l’historien des sciences J. Z. Buchwald
(8) de déterminer avec précision l’acuité visuelle de Fresnel ! Une difficulté est qu’il opère d’abord en lumière blanche pour des raisons d’intensité (par la suite il travaillera avec des filtres). Il est donc en présence d’un système compliqué de franges polychromes. D’où son alinéa 12 (p. 15) :
Je m’étais assuré d’avance, en dirigeant sur le globule des rayons rouges et ensuite des rayons violets, que les franges produites par ceux-ci s’écartaient moins de l’ombre que celles que donnaient les rayons rouges ... J’ai toujours pris le passage du rouge au violet pour la ligne de séparation des couleurs du premier et du second ordre.
(La longueur d’onde du rouge est double de celle du violet.)
Premières observations, premiers résultats
Pour la discussion, nous représentons en figure 4 le schéma du dispositif.
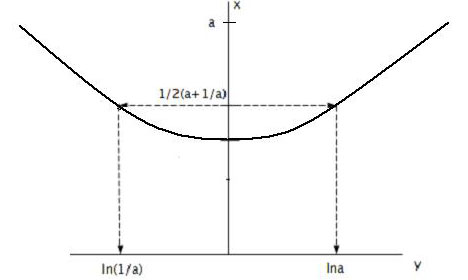
Figure 4 : Schéma du dispositif initial de Fresnel et des rayons en interférences.
Dans le premier dispositif, R est le « point radiant », source de lumière. AA’ est la section du fil diffringent, lui même perpendiculaire au plan de la figure, à la distance a de la source et de largeur c « a. Il observe sur un plan FT’ à la distance b » c du fil. Dans tout ce travail il analyse les effets d’interférences et diffraction de rayons très proches angulairement (ce que l’on nomme « diffraction de Fresnel »). F est un point d’observation extérieur à l’ombre géométrique TT’ tel que FT = x « b, M un point d’observation à l’intérieur de cette ombre tel que TM = y « b. Il évalue la position de l’ombre géométrique, position des points T et T’, par la géométrie, évidente sur la figure.
Il y a deux ensembles de franges : des franges extérieures à l’ombre géométrique du fil et des franges intérieures à celle-ci, comme on le voit sur la figure 5.
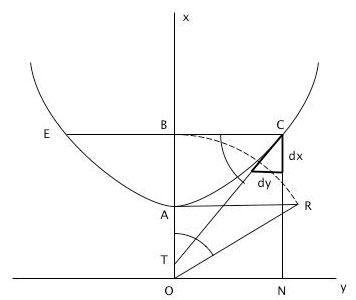
Figure 5 : Franges extérieures et intérieures produites par un fil. T et T’ sont les bords de l’ombre géométrique (simulation numérique)
Cela le mène à une observation cruciale (§15) lorsqu’il « prolonge » une moitié du fil, à droite ou à gauche, le transformant ainsi en un demi-plan :
J’avais collé plusieurs fois un petit carré de papier noir sur un côté du fil de fer, ... et j’avais toujours vu les franges intérieures de l’ombre disparaître ... J'ai fait sur le champ cette réflexion: puisqu'en interceptant la lumière d'un côté du fil, on fait disparaître les franges intérieures, le concours des rayons qui arrivent des deux côtés est nécessaire à leur production.
Les franges extérieures sont aussi modifiées, comme on le voit sur la figure 6. Ce nécessaire « concours de rayons » est, en germe, ce qu'Arago sera fier de nommer quelque temps plus tard des interférences, terme puisé dans le mémoire d’Young.
Figure 6 : a) Ombre portée d'un fil (diffraction par un fil fin symétrique) ; b) Diffraction par le bord d'un écran (que l’on peut aussi considérer comme un fil dont un côté est caché). Les rayons lumineux en interférence sont complètement différents dans les deux cas, ce que démontre la différence des images. (Doc. Institut d’Optique)
Premiers succès de la théorie
Comment expliquer les franges et leur position?
C’est la rencontre, le croisement même de ces rayons qui produisent les franges. ... Les vibrations des rayons qui se croisent peuvent se contrarier lorsque les ventres [de chacune] sont en opposition et se fortifier mutuellement, au contraire, lorsque leurs mouvements sont en harmonie.
Fresnel songe d’abord à l’interférence entre deux rayons.
Pour les franges extérieures de la figure 4, il calcule la différence de marche entre le rayon arrivant directement de R en F et celui issu du bord A. Au plus bas ordre en
x = FT et en
c, la différence de marche
d = RA + AF – RF est telle que
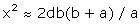
, comme le montre un calcul géométrique simple. Par conséquent, on doit observer des franges brillantes (interférences constructives) pour
d = nλ et des franges sombres pour
d = (2n+1)λ/2, n entier positif, soit des franges situées respectivement en
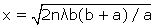 et en
et en 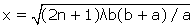 . (1)
. (1)
Cela semble bien confirmé par les mesures. Pour les franges intérieures, ce sont les rayons AM et A’M qui interfèrent. Si y est l’abscisse de M, un calcul géométrique simple donne pour position y des franges brillantes dans la même approximation
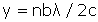 (2)
(2)
soit des franges équidistantes effectivement observées (alinéas 28-30).
En variant les distances a et b, Fresnel remarque avec intérêt (§21 et 22) que les franges extérieures (de tous les ordres)
«... ne se propagent pas en ligne droite, mais suivant des hyperboles dont les foyers sont au point lumineux et au bord du fil. »
Ce résultat se lit sur ses hypothèses. Les franges extérieures sont disposées suivant des courbes telles que FR – FA=
d + RA soit constant, un multiple entier de λ, c'est-à-dire sur une famille d’hyperboles
(9) (RA est constant). De même pour les franges intérieures : MA’– MA=
nλ.
Quand Fresnel dit que les franges « se propagent », il compare à ce que l’on attendrait de la part d’ombres, en précisant bien qu’il s’agit du lieu géométrique de ces franges.
En examinant les tableaux de résultats expérimentaux, on est, comme Fresnel, tenté de conclure que c’est là une magnifique théorie, en parfait accord avec l’expérience.
Calcul d’interférences à deux rayons
Fresnel fait, comme on l’a dit, ses calculs sur des interférences à deux rayons, conformément à ce qu’il indique en §16 :
« À l’extérieur les franges sont produites par le croisement des rayons partant du point lumineux et des bords du fil, et dans l’intérieur de l’ombre elles proviennent u croisement des rayons infléchis de chaque côté par les bords du fil. »
On reprend les notations de la figure 4, et on note la différence de marche d = RA + AF – RF (pour un point externe), θ l’angle(RA,RF), β l’angle (RC,RF). En appliquant l’égalité triangulaire :
AF² = RF² + RA² -2RA.RF.cosθ AF² = (RF-RA)² +2RA.RF.(1-cos θ) AF² = (AF-d)² +2RA.RF.(1-cos θ)
En supprimant les termes en d², et en développant θ (d et θ petits):
2AF.d = RA.RF. θ²
Or β et θ sont petits, on peut écrire: β = tg β = y/(a+b), et β + θ = tg (β + θ)= (x+y)/(a+b), d’où θ = x/(a+b); on déduit:
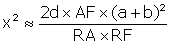
Or RF = (a+b) cos(β+ θ) = (a+b) + 2nd ordre, on peut prendre RF ≈ (a+b) (on reste au second ordre en d à droite en prenant cette approximation) ; de même AF ≈ b et RA ≈ a, soit :
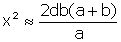
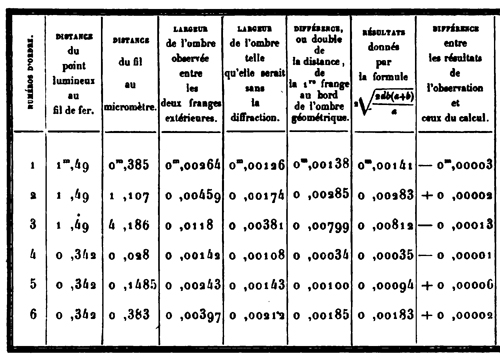
On observe en avant-dernière colonne de §21 les résultats obtenus par Fresnel suivant la formule ci-dessus, et en dernière colonne la différence (minime) entre le calcul et la mesure avec le micromètre (troisième colonne en partant de la gauche) :
La différence de marche de la figure 7 (voir texte ci-après) peut aussi s’exprimer suivant une formule analogue, utilisant l’égalité triangulaire Pn² = PC² + Cn² - 2PC.CN.cosθ Soit, en posant δ = nS :
(b+ δ)² = (a+b)² + a² - 2(a+b)acosθ
au plus bas ordre en δ (δ petit devant b), on a :
b² + 2bδ = (a+b)² + a² - 2 (a+b)a + 2(a+b)a (1-cosθ)
soit
2bδ = 2(a+b)a (1-cosθ)
et, puisque θ est petit :
bδ = (a+b)aθ²/2
Or l’abscisse curviligne sur le cercle z = Mn = aθ, donc :
δ = z² (a+b)/2ab
La théorie s’écroule et renaît
Parfait, pas tout à fait, ou pas du tout ? Fresnel a remarqué quelques différences minimes. La plus importante est la suivante, plus clairement exprimée dans son mémoire de 1818 que dans celui-ci. Reprenons la formule (1) ci-dessus et suivons ses analyses :
D’après la formule ci-dessus, la valeur de x qui correspond au point le plus sombre de la bande obscure du premier ordre, devrait être
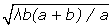
Mais il résulte au contraire de l’observation, que c’est à peu près l’endroit le plus brillant de la première frange. D’après la même théorie, le bord de l’ombre géométrique, où la différence des chemins parcourus est nulle, devrait être plus brillant que le reste de la frange, et c’est précisément le point le plus sombre en dehors de l’ombre géométrique. En général, la position des bandes obscures et brillantes déduite de cette formule est presque exactement inverse de celle que donne l’expérience.
Les différences sont minimes en valeur absolue, c’est grâce à la précision de ses manipulations que Fresnel peut être certain de cette affirmation. Il a calculé en fonction de a, b et c la position précise de l’ombre géométrique, ce qui décale légèrement les choses. Sa théorie est fausse ! Mais il sait être pragmatique :
C’est là la première difficulté que rencontre cette théorie. Pour la lever, il faut supposer que les rayons réfléchis sur le bord de l’écran éprouvent un retard d’une demi-ondulation ; alors on doit ajouter λ/2 à la différence d des chemins parcourus, et la formule générale devient
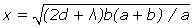
Cette idée est ingénieuse. Bien des théoriciens s’en seraient contentés, en avançant de savants arguments sur l’interaction entre les molécules du fil et celles de la lumière.
Mais la réponse est ailleurs. L’élément déclencheur de la vraie théorie de Fresnel est difficile à dater avec précision. Il s’est produit entre la publication de ce mémoire et de celui de 1818, couronné par l’Académie, où Fresnel parle véritablement de théorie « complète » de la lumière ; plus précisément, entre 1815 et son pli cacheté du 20 avril 1818.
La théorie complète
Fresnel comprend que ses calculs proviennent d’une approximation où deux rayons et deux seuls entrent en interférence. Il lui faut généraliser cela à un ensemble de rayons, à une onde tout entière.
La réponse se trouve dans le principe de Huygens. Il deviendra le principe de Huygens-Fresnel, ainsi nommé par Kirchhoff et Bunsen en 1870. La formulation de ce principe, que Fresnel présente dans son pli cacheté comme allant de soi, est la suivante :
La théorie des ondulations ... conduit à une explication complète des phénomènes, au moyen du principe d’Huygens qu’on peut énoncer ainsi : les vibrations d’une onde lumineuse dans chacun de ses de ses points sont égales à la somme de tous les mouvements élémentaires qu’y enverrait au même instant, en agissant isolément, chaque petite partie de cette onde considérée dans une quelconque de ses positions antérieures.
L’idée d’utiliser le principe d’Huygens est venue à Fresnel dans un des multiples échanges qu’il a eus pendant les trois années séparant les deux mémoires. Il est possible que tout simplement quelqu’un ait fait allusion aux travaux d’Huygens comme partie intégrante des idées sur la lumière et que Fresnel, penaud de les avoir ignorés, se soit rapidement mis à la page. On ne trouve pas de lettre d’Arago sur ce sujet. Fresnel n’en parle à son frère Léonor qu’en 1816.
Le résultat est contenu dans le mémoire de 1818 couronné par l’Académie. Il y est présenté dans la deuxième partie, de manière un peu théâtrale, comme débouchant sur la véritable théorie, après une longue analyse des imperfections de la théorie à deux rayons (cas particulier applicable aux trous d’Young).
Reprenons la diffraction par un écran infini, représenté sur la figure 7, tirée du mémoire de 1818
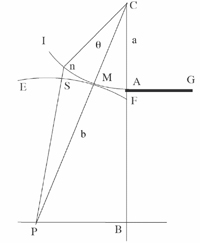
Figure 7 : Diffraction par un demi-plan infini AG.
Dans cette figure, C est maintenant la source, et P le point d’observation. M, appelé « pôle » par Fresnel, est l’intersection du cercle AMI, de rayon a centré en C, avec la droite CP. Sur ce cercle, les ondes émises en C sont toutes en phase et d’égale intensité. Le cercle FME est centré en P et de rayon b.
L’angle θ est représenté pour la commodité. On veut évaluer la différence de marche
δ entre CnP et CMP soit Pn+nC-PC, notée nS sur la figure, au plus bas ordre en fonction de l’abscisse curviligne
z=Mn=
aθ. Un calcul géométrique sur le triangle PnC (voir encadré ci-dessus) donne au plus bas ordre
 . (3)
. (3)
Fresnel introduit alors une représentation des amplitudes lumineuses périodique dans le temps et dans l’espace, c’est à dire une représentation de la propagation des vibrations, du type
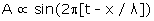
où t est le temps en unité égale à la fréquence. Il s’agit maintenant, d’après le principe de Huygens, de sommer les amplitudes élémentaires provenant de tous les points du cercle AMI. L’amplitude provenant de tout point n est
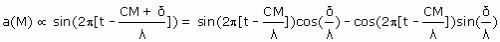
Elle comporte deux termes en quadrature de phase, chacun étant une même oscillation (quel que soit le point n), multipliée par une amplitude obtenue en remplaçant la valeur (3) dans les termes ci-dessus :
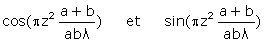 . (5)
. (5)
La somme de toutes les amplitudes va, elle aussi, être une somme de deux termes en quadrature de phase, d’amplitudes respectives
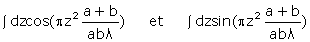 , (6)
, (6)
où apparaissent les célèbres intégrales de Fresnel. L’intégration porte sur l’intervalle
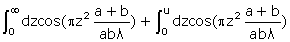
où u correspond à l’abscisse curviligne AM du point A, comptée depuis l’origine en M(10) (on notera en effet que les rayons passant par deux points n et n’ du cercle AMI symétriques par rapport à M ont la même différence de marche).
Ces intégrales (6) sont des fonctions transcendantes de u, mais on sait qu’elles valent toutes deux ½ dans le cas particulier u=0 (et (a+b)/abλ =1/2). Fresnel se met donc à les calculer numériquement, à la main, « d’une façon commode » par des développements en série, avec une précision de quelques dix-millièmes
(11) !
Le résultat est spectaculaire. L’intensité lumineuse est proportionnelle au carré de l’amplitude, soit à
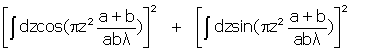
(lorsque l’on moyenne sur le temps, pour des temps très supérieurs à la période, le terme croisé du carré de l’amplitude (4) s’élimine).
Toutes les imperfections de la théorie des deux rayons disparaissent. Théorie et expérience sont en plein accord, à la précision tant de la mesure que du calcul !
Le point blanc de Poisson
Les débats sont acharnés. Laplace, Biot, Poisson, partisans de la théorie de l'émission sont sceptiques, Arago et Gay-Lussac sont enthousiastes.
On vit un moment de stupéfaction quand Poisson fait remarquer que la théorie prévoit qu'au centre de l'ombre d'un petit disque circulaire, ou d’une sphère opaques, les intégrales de Fresnel se calculent facilement et qu’on devrait voir, paradoxalement, un point brillant. Notons que la simple symétrie du problème montre qu’en effet tous les rayons sont en phase sur cet axe et qu’ils y interfèrent constructivement. Fresnel et Arago font immédiatement l'expérience et confirment cette prévision étonnante (figure 8) vraiment contraire à la théorie de l’émission. La stupéfaction cède la place à l’enthousiasme, et Laplace félicite publiquement Fresnel.
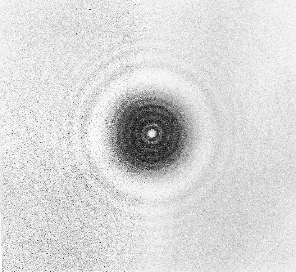
Figure 8 : Point brillant au centre de l'ombre d'un disque ou d’une sphère (Doc. Institut d’Optique.)
La notoriété scientifique
De 1814 à 1815, Fresnel a travaillé sans connaître les travaux d’Young. Il est dépité d'apprendre en 1816 par Arago qui a visité l'Angleterre avec Gay-Lussac, après le blocus, que les travaux d’Young, antérieurs aux siens, aboutissent aux mêmes résultats, mais il est beau joueur. Il écrira à Young
(12)Ce que vous m'avez laissé à faire était aussi difficile que ce que vous aviez fait. Vous aviez cueilli les fleurs, j'ai creusé avec peine pour atteindre les racines...
Il aura par la suite de nombreux échanges avec Young avec qui il se liera d’amitié.
En 1816 Arago fait mettre à sa disposition la « chambre obscure » de l'Ecole Polytechnique dotée d'un héliostat. En mars, Fresnel réalise la célèbre expérience d’interférences dite « des miroirs de Fresnel » de même nature mais plus précise que celle des trous d’Young.
Les travaux d’Young n'avaient en aucune façon la profondeur de ceux de Fresnel, ni sur le plan expérimental, ni sur celui de l'analyse théorique. Young, pragmatique, n'avait pas le talent expérimental de Fresnel, ni le sens de l'estimation des erreurs. Laplace a dit de lui: « Young n'a jamais bien compris la différence qu'il y a entre un aperçu des choses et une véritable démonstration. »
La première gloire de Fresnel, qui est ingénieur rappelons-le, vient donc en 1819. L'Académie des sciences avait décidé en 1817 de consacrer son grand prix des sciences mathématiques à l'étude expérimentale et théorique des phénomènes de diffraction. Fresnel, encouragé par Arago et Ampère, présente un mémoire et gagne (on doit à la vérité de dire que deux projets seuls étaient soumis dont un manifestement faux). Les rapporteurs sont Laplace, Biot, Poisson, Arago et Gay-Lussac.
Le principe de Huygens, qui deviendra le Principe de Huygens-Fresnel, trouve sa formulation complète. Chaque élément d’une surface d'onde peut être considéré comme émettant à son tour des ondes élémentaires. Mais la grande différence est que ces ondes vont interférer ce qui va expliquer les maxima et minima des franges d'interférences et de diffraction.
Un triomphe est que Fresnel peut ainsi expliquer le rayon lumineux dans le cadre de la théorie ondulatoire. L'interférence des ondes en dehors d’une faible région autour de la direction principale du rayon lumineux est destructive. Le rayon lumineux, de nature ondulatoire, préserve dans sa propagation sa définition géométrique, dans des limites bien définies et calculables, déterminées par la diffraction.
Soulignons qu’à la fin du mémoire on peut lire les trois remarques suivantes que nous ne commenterons pas ici.
- Par des arguments de cohérence, Fresnel montre la loi de la réflexion.
- De même il démontre la loi de la réfraction en supposant que la vitesse de la lumière est plus faible dans un milieu matériel que dans le vide (contrairement à Newton et à Descartes, pour qui un rayon devait être « attiré » par le milieu, et la vitesse plus grande) :
Je tire de cette théorie une conséquence absolument opposée à celle de Newton : c’est que la marche de la lumière est plus lente dans le verre que dans l’air, suivant le rapport du sinus de réfraction à celui d’incidence.
- Enfin, dans son alinéa 44, on trouve la constatation :
Une conséquence remarquable de ce principe, c’est que le chemin que suit la lumière en se réfractant est celui qui l’amène le plus promptement d’un point pris dans l’air à un autre point pris dans le verre.
Cela n’est autre que le principe de Fermat ! Il y a fort à penser, Lagrange ayant enseigné à l’Ecole Polytechnique à ses débuts, que Fresnel connaissait cette idée. Il est néanmoins curieux qu’il ne mentionne jamais Fermat dans ses écrits.
Polarisation et optique des milieux anisotropes
En mai 1818, Fresnel se plonge sur les phénomènes de polarisation. Il établit la transversalité des vibrations lumineuses de « l’éther », d’abord très controversée, même par Arago. Les ondes lumineuses sont fondamentalement différentes des ondes sonores, longitudinales.
À partir de 1819, avec Arago, il entreprend une étude systématique de la double réfraction et des propriétés de polarisation associées. Il formalise complètement la notion d'ondes lumineuses et la notion de polarisation.
Dans une série de mémoires s'échelonnant entre le 19 novembre 1821 et le 31 mars 1822, Fresnel met au point la théorie de la double réfraction dans les cristaux uniaxes et biaxes
(13). Il introduit les notions de surface des indices et d'ellipsoïde des indices qui portent son nom.
Fresnel est élu à l'Académie des Sciences le 12 Mai 1823 à l’unanimité. Mais sa santé décline rapidement, et il se sent débordé par la multiplicité de ses tâches. À l’issue d'une session d'examens oraux à l'Ecole Polytechnique, dont il parle à Young en soulignant « ... je suis accablé par la fatigue et le besoin de sommeil... », il est frappé par une forte crise d'hémoptysie.
Il cesse son travail scientifique en 1825 et ne se consacre plus qu'à son métier d'ingénieur. Une semaine avant sa mort, en 1827, Arago, son ami, admirateur et protecteur, vient lui présenter la médaille Rumford que lui a décernée la Royal Society en le nommant membre associé.

(1)Les écoles centrales sont créées par la Convention en 1795 (sur rapport de Lakanal) dans chaque département, en même temps que les écoles primaires. L’École centrale de Caen est devenue le lycée Malherbe.
(2)L’imprimatur est une autorisation de publier donnée par la hiérarchie catholique à un de ses membres. Elle existe toujours de nos jours. Le terme est aussi passé dans le langage courant, comme le « Nihil Obstat » (« rien ne s’y oppose ») qui était la réponse autorisant la publication.
(4) Il écrivit des articles sur la vision et le fonctionnement de l’oeil. Il expliqua le mouvement des fluides et les marées, l'arc-en-ciel, la capillarité. En découvrant le premier que certains mots de la pierre de Rosette sont écrits de manière phonétique, il prépara les travaux de Champollion sur les hiéroglyphes.
(5)Cette expression se trouve dans l’Eloge prononcé par Arago, le 26 juillet 1830 (la veille des Trois Glorieuses). Ce discours « mérite le détour » :
http://www.academie-sciences.fr/membres/in_memoriam/Fresnel/Fresnel_oeuvre.htm
(6)Cette notion existe dans les Réflexions sur la puissance motrice du feu de Sadi Carnot.
(7)Cette « rotation » ne possède que deux valeurs : elle est alignée soit dans la direction de propagation du photon, soit en sens inverse. ces deux états correspondent à la polarisation circulaire droite ou gauche de la lumière, dont on construit un état général par superposition. En ce sens, la polarisation de la lumière est le seul phénomène quantique visible à l’oeil nu ! C’est, entre autres, une propriété très exploitée à notre époque dans l’aventure de « l’Information quantique ».
(8)J. Z. Buchwald, The rise of the Wave Theory of Light, The University of Chicago Press, 1984; page 124
(9) Une hyperbole de foyers A et B est l’ensemble des points M tels que MA – MB = constante.
(10)Le terme de gauche correspond à l’intégration à gauche de M, le terme de droite à l’intégration à droite de M, c'est-à-dire entre M et A.
(11) J. Z. Buchwald op. cit. page 167
(12)La correspondance de Fresnel et Young se trouve dans le volume 2 des Oeuvres complètes. La présente lettre, du 26 novembre 1824, est le document LVI, en page 768.








![]() et en
et en ![]() . (1)
. (1)![]() (2)
(2)![]()
![]()
![]()

![]()
![]()

![]() . (3)
. (3)![]()
![]()
![]() . (5)
. (5)![]() , (6)
, (6)![]()
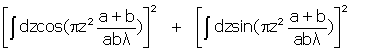


 Une version numérisée par Google du Volume 1 d’où est tiré l’article analysé ici se trouve sur : http://books.google.fr/books?id=3QgAAAAAMAAJ
Une version numérisée par Google du Volume 1 d’où est tiré l’article analysé ici se trouve sur : http://books.google.fr/books?id=3QgAAAAAMAAJ Une version numérisee par Gallica du Volume 2 (qui contient le mémoire de juillet 1818, couronné par l’Académie en 1819) se trouve sur : http://gallica.bnf.fr/ark:/12148/bpt6k91937w
Une version numérisee par Gallica du Volume 2 (qui contient le mémoire de juillet 1818, couronné par l’Académie en 1819) se trouve sur : http://gallica.bnf.fr/ark:/12148/bpt6k91937w L’Académie des sciences a fait une page d’hommage à Fresnel (dont le lien vers le même mémoire de 1818): http://www.academie-sciences.fr/Membres/in_memoriam/Fresnel/Fresnel_oeuvre.htm Elle permet d’accéder au Volume 3, consacré entièrement au travail d’ingénieur de Fresnel, à ces célèbres lentilles à échelons et à l’élaboration de phares, qui révolutionnèrent la sécurité de la navigation.
L’Académie des sciences a fait une page d’hommage à Fresnel (dont le lien vers le même mémoire de 1818): http://www.academie-sciences.fr/Membres/in_memoriam/Fresnel/Fresnel_oeuvre.htm Elle permet d’accéder au Volume 3, consacré entièrement au travail d’ingénieur de Fresnel, à ces célèbres lentilles à échelons et à l’élaboration de phares, qui révolutionnèrent la sécurité de la navigation. Jed Z. Buchwald, The Rise of the Wave Theory of Light, The University of Chicago Press, 1984.
Jed Z. Buchwald, The Rise of the Wave Theory of Light, The University of Chicago Press, 1984. James Lequeux, François Arago, un savant généreux, Physique et astronomie au XIXe siècle, EDP Sciences, Paris 2008.
James Lequeux, François Arago, un savant généreux, Physique et astronomie au XIXe siècle, EDP Sciences, Paris 2008. L’édition en latin de l’ouvrage de Francesco Maria Grimaldi, Physico-mathesis de lumine, coloribus, et iride se trouve sur la bibliothèque numérique de l’Instituto e Museo di Storia della Scienza à Florence http://fermi.imss.fi.it/rd/bdv?/bdviewer/bid=300682# (voir notamment les propositions XXI et XXII).
L’édition en latin de l’ouvrage de Francesco Maria Grimaldi, Physico-mathesis de lumine, coloribus, et iride se trouve sur la bibliothèque numérique de l’Instituto e Museo di Storia della Scienza à Florence http://fermi.imss.fi.it/rd/bdv?/bdviewer/bid=300682# (voir notamment les propositions XXI et XXII).





